 θεωρούμε σημείο
θεωρούμε σημείο 
Μεταβλητή ευθεία
 διέρχεται από το
διέρχεται από το  και τέμνει τις πλευρές της γωνίας στα σημεία
και τέμνει τις πλευρές της γωνίας στα σημεία 
Να βρεθεί η θέση της ευθείας στην οποία το εμβαδόν του τριγώνου
 γίνεται ελάχιστο.
γίνεται ελάχιστο.Ομοίως, αν το σημείο
 αντικατασταθεί από κύκλο κέντρου
αντικατασταθεί από κύκλο κέντρου  και η ευθεία
και η ευθεία  από εφαπτομένη του κύκλου.
από εφαπτομένη του κύκλου.Και απαντήσαμε εδώ: viewtopic.php?f=62&t=65893

 , το οποίο έχει σταθερό εμβαδόν .
, το οποίο έχει σταθερό εμβαδόν . . Τα τρίγωνα είναι όμοια και από :
. Τα τρίγωνα είναι όμοια και από :  , παίρνω :
, παίρνω :  .
. ,
, , συνεπώς
, συνεπώς 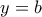 , δηλαδή το
, δηλαδή το  .
. η προβολή του
η προβολή του 
 το αντιδιαμετρικό του
το αντιδιαμετρικό του 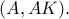
 που τέμνει την
που τέμνει την  στο
στο  Η
Η 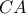 που τέμνει την
που τέμνει την  είναι η ζητούμενη ευθεία.
είναι η ζητούμενη ευθεία. στα
στα  αντίστοιχα και την
αντίστοιχα και την  στο
στο 


 .
. είναι το μέσο του
είναι το μέσο του  .
. , άρα αρκεί να ελαχιστοποιήσουμε το
, άρα αρκεί να ελαχιστοποιήσουμε το 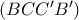 ...
... (δηλαδή προεκτείνουμε την
(δηλαδή προεκτείνουμε την  κατά
κατά  και φέρνουμε παράλληλλες από το
και φέρνουμε παράλληλλες από το  προς τις δοθείσες ευθείες). Η άλλη διαγώνιος
προς τις δοθείσες ευθείες). Η άλλη διαγώνιος  από το
από το  . τα υπόλοιπα έπονται.
. τα υπόλοιπα έπονται. , της οποίας το σημείο
, της οποίας το σημείο  σημείο του
σημείο του  ,
, στο σημείο
στο σημείο  . Τώρα έχουμε* :
. Τώρα έχουμε* : 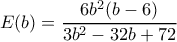
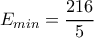 , για
, για  . Αλλά τότε είναι
. Αλλά τότε είναι 
 , είναι το μέσο του
, είναι το μέσο του  .
.
 είναι
είναι 
 (1)
(1)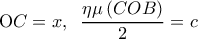 , με
, με  θετικές σταθερές και
θετικές σταθερές και  .
. .
. .
. είναι ίση με
είναι ίση με  . Τότε
. Τότε  , που συμβαίνει όταν το
, που συμβαίνει όταν το