


και αν
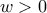 και
και  , να αποδείξετε ότι:
, να αποδείξετε ότι:(α)

(b) Οι αριθμοί
 δεν είναι δυνατόν να είναι ομόσημοι
δεν είναι δυνατόν να είναι ομόσημοι


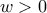 και
και  , να αποδείξετε ότι:
, να αποδείξετε ότι:
 δεν είναι δυνατόν να είναι ομόσημοι
δεν είναι δυνατόν να είναι ομόσημοιΑπό την πρώτη σχέση παίρνουμε:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:Αν
και ανκαι
, να αποδείξετε ότι:
(α)
(b) Οι αριθμοίδεν είναι δυνατόν να είναι ομόσημοι




 παίρνουμε:
παίρνουμε:


 . Όμοια από την τρίτη σχέση και την
. Όμοια από την τρίτη σχέση και την  παίρνουμε:
παίρνουμε:

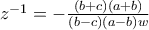

 προκύπτει το ζητούμενο.
προκύπτει το ζητούμενο.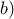 τώρα θα αξιοποιήσουμε την γνωστή ιδιότητα: To γινόμενο δύο θετικών αριθμών είναι θετικός.
τώρα θα αξιοποιήσουμε την γνωστή ιδιότητα: To γινόμενο δύο θετικών αριθμών είναι θετικός. περιπτώσεις:
περιπτώσεις: Και οι τρεις είναι θετικοί. Τότε
Και οι τρεις είναι θετικοί. Τότε 



 (αφού
(αφού  θετικός και συνεπώς η ύπαρξή του δεν επηρεάζει το πρόσημο),
θετικός και συνεπώς η ύπαρξή του δεν επηρεάζει το πρόσημο), 

 Από τις δύο παραπάνω σχέσεις και με βάση την προαναφερθείσα ιδιότητα λαμβάνουμε:
Από τις δύο παραπάνω σχέσεις και με βάση την προαναφερθείσα ιδιότητα λαμβάνουμε:  . Όμως αφού
. Όμως αφού  παίρνουμε
παίρνουμε 

 . Συνεπώς, σε αυτήν την περίπτωση οι
. Συνεπώς, σε αυτήν την περίπτωση οι  δεν είναι ομόσημοι.
δεν είναι ομόσημοι. Και οι τρεις είναι αρνητικοί. Ισχύει πως αν
Και οι τρεις είναι αρνητικοί. Ισχύει πως αν  τότε
τότε  . Συνεπώς, υποθέτουμε ότι
. Συνεπώς, υποθέτουμε ότι  , τότε
, τότε  , άτοπο , αφού στο πρώτο ερώτημα δείξαμε ότι
, άτοπο , αφού στο πρώτο ερώτημα δείξαμε ότι  .
.  δεν γίνεται να είναι ομόσημοι.
δεν γίνεται να είναι ομόσημοι.έχουμεJimNt. έγραψε: Από την πρώτη σχέση παίρνουμε:


 , και λοιπά.
, και λοιπά.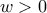 .
.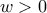 "
"Νομίζω λύνεται παίρνοντας περιπτώσεις:Mihalis_Lambrou έγραψε:Ωραιότατα.
Λίγο αλλιώς το b).
Πολλαπλασιάζοντας κατά μέλη τα
έχουμεJimNt. έγραψε: Από την πρώτη σχέση παίρνουμε:


, και λοιπά.
Ας προσθέσω ότι και στους δύο συλλογισμούς έγινε χρήση της υπόθεσης.
To αφήνω ως άσκηση "να αποδειχθεί το (b) της αρχικής ερώτησης δίχως να υποθέσουμε ότι"
 για
για 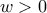 . Συνεπώς, έχουμε και την περιπτώση:
. Συνεπώς, έχουμε και την περιπτώση: (για
(για  τα
τα 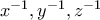 δεν ορίζονται) Διακρίνουμε τις ύποπεριπτώσεις:
δεν ορίζονται) Διακρίνουμε τις ύποπεριπτώσεις:
 τότε
τότε  , άτοπο, αφού
, άτοπο, αφού 

 . Έχουμε
. Έχουμε 

 (διαιρέσαμε με
(διαιρέσαμε με  και τα δύο μέλη και συνεπώς η φορά της ανίσωσης άλλαξε) και
και τα δύο μέλη και συνεπώς η φορά της ανίσωσης άλλαξε) και 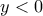

 . Τώρα με βάση την προαναφερθείσα ιδιότητα:
. Τώρα με βάση την προαναφερθείσα ιδιότητα:





 (αλλάζει η φορά επειδή πολλαπλασιάσαμε με αρνητικό αριθμό και τα δύο μέλη (τον
(αλλάζει η φορά επειδή πολλαπλασιάσαμε με αρνητικό αριθμό και τα δύο μέλη (τον  )), άτοπο. Συνεπώς, σε καμία περίπτωση δεν είναι εφικτό οι
)), άτοπο. Συνεπώς, σε καμία περίπτωση δεν είναι εφικτό οι  να είναι ομόσημοι.
να είναι ομόσημοι. ότι αν οι
ότι αν οι  είναι ομόσημοι τότε ο
είναι ομόσημοι τότε ο  θα είχε και αυτός το ίδιο πρόσημο με τους τρεις. Ειδικά, το γινόμενο
θα είχε και αυτός το ίδιο πρόσημο με τους τρεις. Ειδικά, το γινόμενο  , σε αυτή την περίπτωση, θα έχει το ίδιο πρόσημο με το
, σε αυτή την περίπτωση, θα έχει το ίδιο πρόσημο με το  .
. που γράφεται
που γράφεται 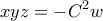 (όπου μάζεψα όλα τα τέλεια τετράγωνα στο
(όπου μάζεψα όλα τα τέλεια τετράγωνα στο  ) δείχνει ότι το
) δείχνει ότι το  και το
και το  έχουν αντίθετα πρόσημα. Άτοπο. Και λοιπά.
έχουν αντίθετα πρόσημα. Άτοπο. Και λοιπά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης