
Η εξίσωση
-
cool geometry
- Δημοσιεύσεις: 292
- Εγγραφή: Τρί Αύγ 02, 2022 7:28 am
-
ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ
- Δημοσιεύσεις: 30
- Εγγραφή: Παρ Απρ 09, 2021 2:41 pm
Re: Η εξίσωση
Βλ. πιο κάτω ανάρτηση.
τελευταία επεξεργασία από ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ σε Δευ Αύγ 08, 2022 8:25 pm, έχει επεξεργασθεί 2 φορές συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Η εξίσωση
Φίλιππε, μπορεί να κάνω λάθος αλλά για ξαναδές αυτό
 , όχι τα άλλα δύο.
, όχι τα άλλα δύο.
και επίσης το
(το τελευταίο βγάζει μόνο το
 , όχι τα άλλα δύο.
, όχι τα άλλα δύο.-
cool geometry
- Δημοσιεύσεις: 292
- Εγγραφή: Τρί Αύγ 02, 2022 7:28 am
-
ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ
- Δημοσιεύσεις: 30
- Εγγραφή: Παρ Απρ 09, 2021 2:41 pm
Re: Η εξίσωση
Επειδή την έλυσα από κινητό, μου διέφυγε η προφανής ανισότητα αριθμητικού-γεωμετρικού μέσου. Πράγματι, προκύπτει το παραπάνω συμπέρασμα που δίνει:  και μετά διάκριση περιπτώσεων. (Μπορούμε να βρούμε κάτω φράγμα για διευκόλυνση της εύρεσης;)
και μετά διάκριση περιπτώσεων. (Μπορούμε να βρούμε κάτω φράγμα για διευκόλυνση της εύρεσης;)
Όσον αφορά στην προηγούμενη λύση μου, πράγματι στην πρώτη περίπτωση, η: στο δεξί μέλος δεν είναι υποχρεωτική και υποθέτει:
στο δεξί μέλος δεν είναι υποχρεωτική και υποθέτει:  .
.
 και μετά διάκριση περιπτώσεων. (Μπορούμε να βρούμε κάτω φράγμα για διευκόλυνση της εύρεσης;)
και μετά διάκριση περιπτώσεων. (Μπορούμε να βρούμε κάτω φράγμα για διευκόλυνση της εύρεσης;)Όσον αφορά στην προηγούμενη λύση μου, πράγματι στην πρώτη περίπτωση, η:
 στο δεξί μέλος δεν είναι υποχρεωτική και υποθέτει:
στο δεξί μέλος δεν είναι υποχρεωτική και υποθέτει:  .
.
τελευταία επεξεργασία από ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ σε Δευ Αύγ 08, 2022 11:54 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Η εξίσωση
Εδώ έχεις ένα σοβαρό λογικό σφάλμα.ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ έγραψε: ↑Δευ Αύγ 08, 2022 8:23 pm... διότι θα μπορούσα εξ' αρχής να υποθέσω διαφορετική διάταξη.
Είναι σαν να λες: Πες ότι σε μία άσκηση έχουμε τρεις άνισους αριθμούς
 που ο πιο μικρός είναι
που ο πιο μικρός είναι  και ο πιο μεγάλος είναι
και ο πιο μεγάλος είναι  . Χωρίς βλάβη μπορώ να υποθέσω ότι
. Χωρίς βλάβη μπορώ να υποθέσω ότι  . Άρα έχω
. Άρα έχω  .
. Θα μπορούσα εξ αρχής, όπως γράφεις, να έχω υποθέσει διαφορετική διάταξη, ας πούμε την
 . Τώρα θα έχω
. Τώρα θα έχω  .
.Υιοθετώντας τώρα τον συλλογισμό που γράφεις παραπάνω, έχουμε
 . Με άλλα λόγια δείξαμε ότι
. Με άλλα λόγια δείξαμε ότι  .
.Εννοείται ότι αυτά δεν στέκουν αλλά βασίζονται σε λογικό σφάλμα.
Για ξαναδές, λοιπόν, το επιχείρημά σου.
-
ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ
- Δημοσιεύσεις: 30
- Εγγραφή: Παρ Απρ 09, 2021 2:41 pm
-
cool geometry
- Δημοσιεύσεις: 292
- Εγγραφή: Τρί Αύγ 02, 2022 7:28 am
Re: Η εξίσωση
Κι εδώ πολύ ωραία, αλλά ούτε κανMihalis_Lambrou έγραψε: ↑Δευ Αύγ 08, 2022 12:22 pmΦίλιππε, μπορεί να κάνω λάθος αλλά για ξαναδές αυτό
Πολύ σωστά. Εφόσον, μπορούμε να πάρουμε
, όχι όμως ότι
και επίσης το(το τελευταίο βγάζει μόνο το, όχι τα άλλα δύο.
 δεν βγαίνει.
δεν βγαίνει.-
cool geometry
- Δημοσιεύσεις: 292
- Εγγραφή: Τρί Αύγ 02, 2022 7:28 am
Re: Η εξίσωση
ΦΙΛΙΠΠΟΣ ΚΑΛΟΥΔΗΣ έγραψε: ↑Δευ Αύγ 08, 2022 8:23 pmΕπειδή την έλυσα από κινητό, μου διέφυγε η προφανής ανισότητα αριθμητικού-γεωμετρικού μέσου. Πράγματι, προκύπτει το παραπάνω συμπέρασμα που δίνει:και μετά διάκριση περιπτώσεων. (Μπορούμε να βρούμε κάτω φράγμα για διευκόλυνση της εύρεσης;)
δυστυχώς το κάτω φράγμα δεν μπορεί να βρεθεί, πρέπει να πάρεις όλες τις περιπτώσεις.
Όσον αφορά στην προηγούμενη λύση μου, πράγματι στην πρώτη περίπτωση, η:στο δεξί μέλος δεν είναι υποχρεωτική και υποθέτει:
.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες

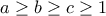 . Τότε, η εξίσωση μου δίνει:
. Τότε, η εξίσωση μου δίνει:  . Άρα:
. Άρα:  Παρατηρώ πως
Παρατηρώ πως  , άρα
, άρα  τέλειο τετράγωνο, οπότε:
τέλειο τετράγωνο, οπότε:  και μετά εξετάζω περιπτώσεις. Αναλυτική λύση αργότερα, καθώς τώρα γράφω από κινητό
και μετά εξετάζω περιπτώσεις. Αναλυτική λύση αργότερα, καθώς τώρα γράφω από κινητό  .
.
 .
.  , άρα
, άρα 

