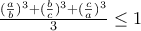
Να βρεθεί το άθροισμα:
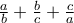
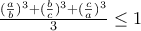
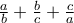
Είναι γνωστό ότι αν
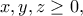 τότε
τότε 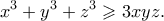 Έτσι η δοθείσα σχέση γράφεται:
Έτσι η δοθείσα σχέση γράφεται: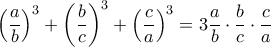
 δεν είναι ίσοι μεταξύ τους, θα είναι
δεν είναι ίσοι μεταξύ τους, θα είναι 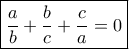
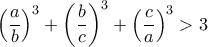

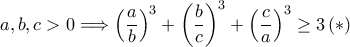
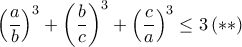
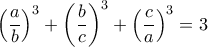

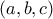 θετικών πραγματικών αριθμών, που είναι τέτοιοι ώστε
θετικών πραγματικών αριθμών, που είναι τέτοιοι ώστε 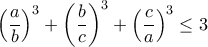 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες