Η σκάλα
Συντονιστές: silouan, Doloros, george visvikis
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Η σκάλα
Ένα κλασικό.
Για μαθητές μέχρι 22/3 και μόνο με ευκλείδεια
Για μαθητές μέχρι 22/3 και μόνο με ευκλείδεια
- Συνημμένα
-
- ΣΚΑΛΑ.JPG (88.55 KiB) Προβλήθηκε 820 φορές
Λέξεις Κλειδιά:
Re: Η σκάλα
Έμεινε αρκετό χρόνο αναπάντητη , γι' αυτό ας μου επιτραπεί μια υπόδειξη : Όταν η σκάλα 
είναι κάθετη στην , έχει προφανώς μήκος
, έχει προφανώς μήκος 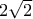 . Αρκεί να δείξουμε ότι για οποιαδήποτε
. Αρκεί να δείξουμε ότι για οποιαδήποτε
διαφορετική θέση της σκάλας , έστω , θα είναι
, θα είναι  ....
....

είναι κάθετη στην
 , έχει προφανώς μήκος
, έχει προφανώς μήκος 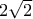 . Αρκεί να δείξουμε ότι για οποιαδήποτε
. Αρκεί να δείξουμε ότι για οποιαδήποτεδιαφορετική θέση της σκάλας , έστω
 , θα είναι
, θα είναι  ....
....- nickchalkida
- Δημοσιεύσεις: 312
- Εγγραφή: Τρί Ιουν 03, 2014 11:59 am
- Επικοινωνία:
Re: Η σκάλα
Σκεπτόμενος να δώσω, όσο το δυνατόν πιο απλό σκεπτικό, κατέληξα στο ακόλουθο.
Για να περάσει η σκάλα, πρέπει να περάσουν όλα τα σημεία της. Άρα πρέπει να περάσει και το μέσον.
Ο γεωμετρικός τόπος όμως του μέσου της σκάλας είναι τo τεταρτοκύκλιο
είναι τo τεταρτοκύκλιο  ,
,
διότι . Δηλαδή για να περάσει το μέσο θα πρέπει
. Δηλαδή για να περάσει το μέσο θα πρέπει  ,
,
που σημαίνει μέγιστο μήκος για τη σκάλα .
.
(Η αιτιολόγηση βασίζεται στην εμπειρική γνώση ότι για να περάσει η σκάλα,
αρκεί να περάσει το μέσον της, υπολείπεται λοιπόν η μαθηματική απόδειξη)
Γενικά άν τυχαίο σημείο της σκάλας
τυχαίο σημείο της σκάλας  και
και  ,
,  , τότε
, τότε
από την ομοιότητα των τριγώνων ,
,  παίρνουμε:
παίρνουμε:

Επομένως, ο γεωμετρικός τόπος τυχόντος σημείου , με αποστάσεις από τα άκρα της σκάλας
, με αποστάσεις από τα άκρα της σκάλας  ,
, 
είναι ελλειψη με τύπο αυτόν που βρέθηκε.
Για να περάσει η σκάλα, πρέπει να περάσουν όλα τα σημεία της. Άρα πρέπει να περάσει και το μέσον.
Ο γεωμετρικός τόπος όμως του μέσου της σκάλας
 είναι τo τεταρτοκύκλιο
είναι τo τεταρτοκύκλιο  ,
,διότι
 . Δηλαδή για να περάσει το μέσο θα πρέπει
. Δηλαδή για να περάσει το μέσο θα πρέπει  ,
,που σημαίνει μέγιστο μήκος για τη σκάλα
 .
.(Η αιτιολόγηση βασίζεται στην εμπειρική γνώση ότι για να περάσει η σκάλα,
αρκεί να περάσει το μέσον της, υπολείπεται λοιπόν η μαθηματική απόδειξη)
Γενικά άν
 τυχαίο σημείο της σκάλας
τυχαίο σημείο της σκάλας  και
και  ,
,  , τότε
, τότεαπό την ομοιότητα των τριγώνων
 ,
,  παίρνουμε:
παίρνουμε:
Επομένως, ο γεωμετρικός τόπος τυχόντος σημείου
 , με αποστάσεις από τα άκρα της σκάλας
, με αποστάσεις από τα άκρα της σκάλας  ,
, 
είναι ελλειψη με τύπο αυτόν που βρέθηκε.
- Συνημμένα
-
- ladder.png (271.97 KiB) Προβλήθηκε 715 φορές
Μη είναι βασιλικήν ατραπόν επί την γεωμετρίαν.
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Η σκάλα
Στο σχήμα του Θανάση και με τη σημείωση στο σχολιασμό του ότι οι σκάλες που είναι σχεδιασμένες είναι
διαφορετικές σκάλες ως προς το μήκος και όχι μια. Το μέγιστο μήκος σκάλας που περνάει ταυτίζεται με το το ελάχιστο
μήκος σκάλας που δεν περνάει. Εκεί έχουμε μια οριακή κατάσταση όπου η σκάλα περνάει και δεν περνάει. Προφανώς μια
σκάλα που δεν περνάει θα ακουμπάει στο
 . Σχηματίζουμε το τεταρτοκύκλιο
. Σχηματίζουμε το τεταρτοκύκλιο 
Αν η
 εφάπτεται στο τεταρτοκύκλιο τότε
εφάπτεται στο τεταρτοκύκλιο τότε  (απλό). Θα δείξουμε ότι αυτό είναι το
(απλό). Θα δείξουμε ότι αυτό είναι το ελάχιστο μήκος σκάλας που δεν περνάει. Πράγματι αν
 είναι μια άλλη σκάλα που δεν περνάει τότε αυτή θα
είναι μια άλλη σκάλα που δεν περνάει τότε αυτή θα τέμνει το τεταρτοκύκλιο σε κάποιο άλλο σημείο εκτός του
 και εσωτερικό του
και εσωτερικό του 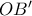 αφού η
αφού η  εφαπτομένη είναι μοναδική. Από ομοιότητα των τριγώνων
εφαπτομένη είναι μοναδική. Από ομοιότητα των τριγώνων  έχουμε
έχουμε  και επομένως το μέσο
και επομένως το μέσο 
του
 είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  δηλαδή το
δηλαδή το  είναι εξωτερικό του τεταρτοκυκλίου.
είναι εξωτερικό του τεταρτοκυκλίου. Άρα

- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Η σκάλα
Καλησπέρα σε όλους. Το ίδιο ερώτημα με τον Λάμπρο θέτουμε με τον Γιάννη Θωμαΐδη στο 3ο κεφάλαιο της "Οδού Μαθηματικής Σκέψης".
Μεταφέρω την διαφορετική προσέγγιση που δίνουμε εκεί (αφήνω τα ελληνικά σύμβολα για να είναι συμβατή η απάντηση με το σχήμα):
Το ερώτημα της εκφώνησης ίσως να μη γίνεται άμεσα κατανοητό από όλους τους μαθητές. Μπορούμε να δώσουμε βοηθήσουμε τους μαθητές να κατανοήσουν το θέμα, περιγράφοντας την κίνηση της σκάλας ως εξής: «Σέρνουμε τη σκάλα κατά μήκος του τοίχου στην ευθεία που ορίζουν τα Ο, Γ. Μόλις αγγίξει η σκάλα στο Γ, τη στρέφουμε με κέντρο περιστροφής το Ο, ώστε η μία της άκρη να αγγίζει τον τοίχο σε σημείο Α. Αν η άλλη άκρη αγγίξει το απέναντι τοίχο σε σημείο Β, τότε η σκάλα δεν μπορεί να στρίψει στη γωνία. Πρέπει, λοιπόν να έχει μήκος μικρότερο από το μικρότερο ευθύγραμμο τμήμα ΑΒ, που διέρχεται από το Ο».
Στο σχολικό βιβλίο δίνονται και οι ακόλουθες υποδείξεις:
i) Να εκφράσετε τα ΟΑ, ΟΒ συναρτήσει της γωνίας θ, .
.
ii) Να αποδείξετε ότι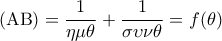 .
.
iii) Να βρείτε την τιμή της γωνίας θ, για την οποία το ΑΒ γίνεται ελάχιστο.
Λύση:
Στο ΔΟΒ είναι
και στο ΑΟΓ είναι ,
,
οπότε .
.
Μπορούμε να αποφύγουμε τα εργαλεία της Ανάλυσης, χρησιμοποιώντας την Ανισότητα Αριθμητικού-Αρμονικού Μέσου.
Ισχύει , με το ίσον όταν
, με το ίσον όταν  , δηλαδή όταν
, δηλαδή όταν  .
.
ΣΧΟΛΙΟ: Στο βιβλίο σε προηγούμενο θέμα δίνονται μερικές αποδείξεις του μεγίστου της συνάρτησης .
.
Εδώ το αφήνω ως ερώτημα να απαντηθεί δίχως παραγώγους. (Αν ήταν "εντός ύλης", θα το λέγαμε απολύτως τετριμμένο).
ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ:
Οι Τ. Andreescu, Ο. Mushkarov, L. Stoyanov στο Geometric Problems on Maxima and Minima, Birkhaüser Boston, 2006 αναφέρουν ότι αν το πλάτος των διαδρόμων είναι α και β αντίστοιχα, και φ η μία από τις γωνίες που σχηματίζει η ΑΒ με τον ένα τοίχο, τότε
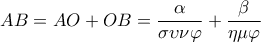 .
.
Η συνάρτηση![\displaystyle f\left( \varphi \right) = \frac{\alpha }{{\sigma \upsilon \nu \varphi }} + \frac{\beta }{{\eta \mu \varphi }},\;\;\;\varphi \in \left[ {0,\;\frac{\pi }{2}} \right] \displaystyle f\left( \varphi \right) = \frac{\alpha }{{\sigma \upsilon \nu \varphi }} + \frac{\beta }{{\eta \mu \varphi }},\;\;\;\varphi \in \left[ {0,\;\frac{\pi }{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/2d1c04e5f04b369b8ba3254a7824e8b6.png) έχει ελάχιστο όταν
έχει ελάχιστο όταν ![\displaystyle \varepsilon \varphi \varphi = \sqrt[3]{{\frac{\beta }{\alpha }}} \displaystyle \varepsilon \varphi \varphi = \sqrt[3]{{\frac{\beta }{\alpha }}}](/forum/ext/geomar/texintegr/latexrender/pictures/d93f358713efb7ffa389680aff92e2e7.png) , την τιμή
, την τιμή  .
.
(Δεν έχω ασχοληθεί με την απόδειξη. Νομίζω πάντως ότι δίχως παραγώγους θα πρέπει να είναι δύσκολη...)
Μεταφέρω την διαφορετική προσέγγιση που δίνουμε εκεί (αφήνω τα ελληνικά σύμβολα για να είναι συμβατή η απάντηση με το σχήμα):
Το ερώτημα της εκφώνησης ίσως να μη γίνεται άμεσα κατανοητό από όλους τους μαθητές. Μπορούμε να δώσουμε βοηθήσουμε τους μαθητές να κατανοήσουν το θέμα, περιγράφοντας την κίνηση της σκάλας ως εξής: «Σέρνουμε τη σκάλα κατά μήκος του τοίχου στην ευθεία που ορίζουν τα Ο, Γ. Μόλις αγγίξει η σκάλα στο Γ, τη στρέφουμε με κέντρο περιστροφής το Ο, ώστε η μία της άκρη να αγγίζει τον τοίχο σε σημείο Α. Αν η άλλη άκρη αγγίξει το απέναντι τοίχο σε σημείο Β, τότε η σκάλα δεν μπορεί να στρίψει στη γωνία. Πρέπει, λοιπόν να έχει μήκος μικρότερο από το μικρότερο ευθύγραμμο τμήμα ΑΒ, που διέρχεται από το Ο».
Στο σχολικό βιβλίο δίνονται και οι ακόλουθες υποδείξεις:
i) Να εκφράσετε τα ΟΑ, ΟΒ συναρτήσει της γωνίας θ,
 .
.ii) Να αποδείξετε ότι
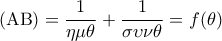 .
.iii) Να βρείτε την τιμή της γωνίας θ, για την οποία το ΑΒ γίνεται ελάχιστο.
Λύση:
Στο ΔΟΒ είναι

και στο ΑΟΓ είναι
 ,
,οπότε
 .
.Μπορούμε να αποφύγουμε τα εργαλεία της Ανάλυσης, χρησιμοποιώντας την Ανισότητα Αριθμητικού-Αρμονικού Μέσου.
Ισχύει
 , με το ίσον όταν
, με το ίσον όταν  , δηλαδή όταν
, δηλαδή όταν  .
. ΣΧΟΛΙΟ: Στο βιβλίο σε προηγούμενο θέμα δίνονται μερικές αποδείξεις του μεγίστου της συνάρτησης
 .
.Εδώ το αφήνω ως ερώτημα να απαντηθεί δίχως παραγώγους. (Αν ήταν "εντός ύλης", θα το λέγαμε απολύτως τετριμμένο).
ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ:
Οι Τ. Andreescu, Ο. Mushkarov, L. Stoyanov στο Geometric Problems on Maxima and Minima, Birkhaüser Boston, 2006 αναφέρουν ότι αν το πλάτος των διαδρόμων είναι α και β αντίστοιχα, και φ η μία από τις γωνίες που σχηματίζει η ΑΒ με τον ένα τοίχο, τότε
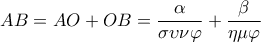 .
.Η συνάρτηση
![\displaystyle f\left( \varphi \right) = \frac{\alpha }{{\sigma \upsilon \nu \varphi }} + \frac{\beta }{{\eta \mu \varphi }},\;\;\;\varphi \in \left[ {0,\;\frac{\pi }{2}} \right] \displaystyle f\left( \varphi \right) = \frac{\alpha }{{\sigma \upsilon \nu \varphi }} + \frac{\beta }{{\eta \mu \varphi }},\;\;\;\varphi \in \left[ {0,\;\frac{\pi }{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/2d1c04e5f04b369b8ba3254a7824e8b6.png) έχει ελάχιστο όταν
έχει ελάχιστο όταν ![\displaystyle \varepsilon \varphi \varphi = \sqrt[3]{{\frac{\beta }{\alpha }}} \displaystyle \varepsilon \varphi \varphi = \sqrt[3]{{\frac{\beta }{\alpha }}}](/forum/ext/geomar/texintegr/latexrender/pictures/d93f358713efb7ffa389680aff92e2e7.png) , την τιμή
, την τιμή  .
.(Δεν έχω ασχοληθεί με την απόδειξη. Νομίζω πάντως ότι δίχως παραγώγους θα πρέπει να είναι δύσκολη...)
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες


 , συνεπώς :
, συνεπώς :  , ό. έ . δ .
, ό. έ . δ .