KARKAR έγραψε: ↑Τρί Ιουν 25, 2019 8:23 am
Στο τρίγωνο

, τα μήκη των πλευρών

και

είναι σταθερά , ενώ εκείνο της

μεταβάλλεται . Βρείτε τη θέση της κορυφής

, για την οποία η γωνία

μεγιστοποιείται . Αφού λύσετε το θέμα για τις δοθείσες τιμές , γενικεύστε .
Καλύτερα να αποφύγετε την παράγωγο !
Καλησπέρα σε όλους. Κάνω πρώτα μια πιο γενικευμένη γενίκευση, εξετάζοντας και τις περιπτώσεις όπου

και

, γράφοντας κατόπιν λίγο πιο αναλυτικά τη σκέψη του
Γιώργου για την περίπτωση
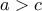
, που υποδεικνύει η εκφώνηση.
Κατόπιν, παραβαίνοντας την υπόδειξη του
Θανάση μελετώ τη γενική περίπτωση, ΔΙΧΩΣ τον ΠΕΡΙΟΡΙΣΜΟ

, χρησιμοποιώντας τη δύναμη της Ανάλυσης.
1η λύση:
Αν

τότε

και δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις

, όταν

.
Αν
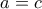
τότε

και επίσης δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις

, όταν

.
Αν
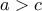
τότε

οπότε

.
Είναι

, για σταθερά θετικά

.
Άρα έχουμε μέγιστη τιμή της γωνίας

, όταν το ημίτονο της γίνει μέγιστο, που συμβαίνει όταν

. Τότε η κορυφή

κινείται στον κύκλο διαμέτρου

.
2η λύση:
Έστω τρίγωνο

με σταθερές πλευρές

και μεταβλητή

, για την οποία ισχύει ο περιορισμός

.
Από Ν. Συνημιτόνων είναι

. Αφού
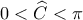
, η συνάρτηση

είναι γνησίως φθίνουσα με πεδίο τιμών
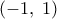
.
Άρα η γωνία

παίρνει τη μέγιστη τιμή της όταν το

πάρει την ελάχιστη τιμή του.
Ζητάμε το ελάχιστο της συνάρτησης

Είναι παραγωγίσιμη με παράγωγο

.
Με πίνακα μεταβολών μονοτονίας βρίσκουμε ότι έχει ελάχιστο όταν

, δηλαδή όταν το τρίγωνο είναι ορθογώνιο με υποτείνουσα την

. H κορυφή

κινείται στον κύκλο διαμέτρου

.
 , τα μήκη των πλευρών
, τα μήκη των πλευρών  και
και  είναι σταθερά , ενώ εκείνο
είναι σταθερά , ενώ εκείνο  μεταβάλλεται . Βρείτε τη θέση της κορυφής
μεταβάλλεται . Βρείτε τη θέση της κορυφής  , για την οποία η γωνία
, για την οποία η γωνία  μεγιστοποιείται .
μεγιστοποιείται .
 η γωνία
η γωνία 
 Άρα η
Άρα η 
 και
και  , γράφοντας κατόπιν λίγο πιο αναλυτικά τη σκέψη του
, γράφοντας κατόπιν λίγο πιο αναλυτικά τη σκέψη του 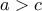 , που υποδεικνύει η εκφώνηση.
, που υποδεικνύει η εκφώνηση. , χρησιμοποιώντας τη δύναμη της Ανάλυσης.
, χρησιμοποιώντας τη δύναμη της Ανάλυσης.  και δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις
και δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις  , όταν
, όταν  .
.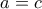 τότε
τότε  και επίσης δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις
και επίσης δεν έχουμε μέγιστη τιμή, ενώ έχουμε άνω φράγμα τις  , όταν
, όταν  .
. οπότε
οπότε  .
. , για σταθερά θετικά
, για σταθερά θετικά  .
.  , όταν το ημίτονο της γίνει μέγιστο, που συμβαίνει όταν
, όταν το ημίτονο της γίνει μέγιστο, που συμβαίνει όταν  . Τότε η κορυφή
. Τότε η κορυφή  .
. με σταθερές πλευρές
με σταθερές πλευρές  , για την οποία ισχύει ο περιορισμός
, για την οποία ισχύει ο περιορισμός  .
. . Αφού
. Αφού 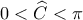 , η συνάρτηση
, η συνάρτηση  είναι γνησίως φθίνουσα με πεδίο τιμών
είναι γνησίως φθίνουσα με πεδίο τιμών 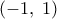 .
. 
 .
. , δηλαδή όταν το τρίγωνο είναι ορθογώνιο με υποτείνουσα την
, δηλαδή όταν το τρίγωνο είναι ορθογώνιο με υποτείνουσα την  . H κορυφή
. H κορυφή  διαμέτρου
διαμέτρου  , που τέμνονται στο
, που τέμνονται στο 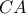 , που είναι εφαπτομένη του
, που είναι εφαπτομένη του  , αφού είναι κάθετη στην
, αφού είναι κάθετη στην  .
. τυχαίο σημείο του
τυχαίο σημείο του  τέμνει τον κύκλο σε δύο σημεία άρα απέχει λιγότερο από το
τέμνει τον κύκλο σε δύο σημεία άρα απέχει λιγότερο από το  , σε σχέση με το
, σε σχέση με το  εμφανίζεται όταν το
εμφανίζεται όταν το  και προφανώς η γωνία
και προφανώς η γωνία  γίνεται μέγιστη αν το
γίνεται μέγιστη αν το  ) , αναζητούμε το ελάχιστο της :
) , αναζητούμε το ελάχιστο της :  .
.
 κ.λ.π.
κ.λ.π. χρησιμοποιώντας την παλιά μέθοδο του σταθερού γινομένου.
χρησιμοποιώντας την παλιά μέθοδο του σταθερού γινομένου. . Οι δύο όροι είναι θετικοί κι έχουν σταθερό γινόμενο, οπότε το άθροισμά τους έχει ελάχιστο όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι.
. Οι δύο όροι είναι θετικοί κι έχουν σταθερό γινόμενο, οπότε το άθροισμά τους έχει ελάχιστο όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι. κ.ο.κ.
κ.ο.κ.