 η διχοτόμος
η διχοτόμος  έχει διπλάσιο μήκος από το ύψος
έχει διπλάσιο μήκος από το ύψος 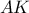 .
.Ο κύκλος
 τέμνει τη πλευρά
τέμνει τη πλευρά  στο σημείο
στο σημείο  και οι ευθείες ,
και οι ευθείες , 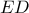 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο 
Βρείτε το λόγο :
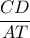 .
.Συντονιστές: silouan, Doloros, george visvikis
 η διχοτόμος
η διχοτόμος  έχει διπλάσιο μήκος από το ύψος
έχει διπλάσιο μήκος από το ύψος 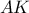 .
. τέμνει τη πλευρά
τέμνει τη πλευρά  στο σημείο
στο σημείο  και οι ευθείες ,
και οι ευθείες , 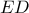 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο 
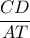 .
.Καλησπέρα κ.Νίκο !
 το συμμετρικό του
το συμμετρικό του  ως προς την
ως προς την  . Τότε, εύκολα προκύπτει πως
. Τότε, εύκολα προκύπτει πως  , καθώς και ότι
, καθώς και ότι  , οπότε
, οπότε  , συνεπώς
, συνεπώς  .
. είναι ισοσκελές τραπέζιο. Οπότε, τα
είναι ισοσκελές τραπέζιο. Οπότε, τα  είναι ομοκυκλικά.
είναι ομοκυκλικά. είναι ίσα (λόγω του συμμετρικού) οπότε αφού τα
είναι ίσα (λόγω του συμμετρικού) οπότε αφού τα  είναι ομοκυκλικά, έχουμε ότι
είναι ομοκυκλικά, έχουμε ότι  .
. .
. .
. είναι όμοια (απλό angle-chasing) οπότε
είναι όμοια (απλό angle-chasing) οπότε  που φυσικά ισούται με τον αριθμό
που φυσικά ισούται με τον αριθμό  !
!Έστω
 Από τον τύπο της διχοτόμου και τη σχέση
Από τον τύπο της διχοτόμου και τη σχέση  έχουμε:
έχουμε:
 άρα
άρα  (*)
(*) και από την ομοιότητα των τριγώνων
και από την ομοιότητα των τριγώνων 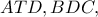

 και η εξίσωση γράφεται:
και η εξίσωση γράφεται: 


Αλλιώς ο υπολογισμός των γωνιών του τριγώνου. Έστω
 Το
Το  είναι το έγκεντρο του
είναι το έγκεντρο του 

 και από το άθροισμα
και από το άθροισμα
 κλπ.
κλπ.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες