Σε τρίγωνο
 οι
οι  είναι οι ακτίνες των παραγγεγραμμένων κύκλων που αντιστοιχούν στις πλευρές
είναι οι ακτίνες των παραγγεγραμμένων κύκλων που αντιστοιχούν στις πλευρές  αντίστοιχα.
αντίστοιχα.Να αποδειχθεί ότι
![\displaystyle\frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{\frac{E^{2}}{r}}\cdot \frac{1}{r} \displaystyle\frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{\frac{E^{2}}{r}}\cdot \frac{1}{r}](/forum/ext/geomar/texintegr/latexrender/pictures/f2900b9a6ecc50d0eec389a38e7eeaf4.png)
όπου
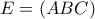 και
και  η ακτίνα του εγγεγραμμένου κύκλου.
η ακτίνα του εγγεγραμμένου κύκλου. οι
οι  είναι οι ακτίνες των παραγγεγραμμένων κύκλων που αντιστοιχούν στις πλευρές
είναι οι ακτίνες των παραγγεγραμμένων κύκλων που αντιστοιχούν στις πλευρές  αντίστοιχα.
αντίστοιχα.![\displaystyle\frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{\frac{E^{2}}{r}}\cdot \frac{1}{r} \displaystyle\frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{\frac{E^{2}}{r}}\cdot \frac{1}{r}](/forum/ext/geomar/texintegr/latexrender/pictures/f2900b9a6ecc50d0eec389a38e7eeaf4.png)
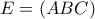 και
και  η ακτίνα του εγγεγραμμένου κύκλου.
η ακτίνα του εγγεγραμμένου κύκλου.![\displaystyle{\boxed{x,y,z>0 \implies \frac{x}{y}+\frac{y}{z}+\frac{z}{x}\geq \frac{x+y+z}{\sqrt[3]{xyz}}}} \displaystyle{\boxed{x,y,z>0 \implies \frac{x}{y}+\frac{y}{z}+\frac{z}{x}\geq \frac{x+y+z}{\sqrt[3]{xyz}}}}](/forum/ext/geomar/texintegr/latexrender/pictures/bb215725c6e4450688220f52ee5a0c15.png)
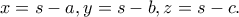
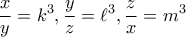 ως
ως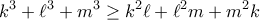
![\displaystyle\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\geq \frac{x+y+z}{\sqrt[3]{xyz}} \displaystyle\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\geq \frac{x+y+z}{\sqrt[3]{xyz}}](/forum/ext/geomar/texintegr/latexrender/pictures/e433df96765e42c6b9b6deb248f8bf53.png) με
με  θετικούς.
θετικούς. το
το  , όπου
, όπου  το
το  , όπου
, όπου  το
το  προκύπτει ότι
προκύπτει ότι ![\displaystyle \frac{y}{x}+\frac{z}{y}+\frac{x}{z}\geq \sqrt[3]{xyz}\left ( \frac{1}{x}+\frac{1}{y} +\frac{1}{z}\right ) \displaystyle \frac{y}{x}+\frac{z}{y}+\frac{x}{z}\geq \sqrt[3]{xyz}\left ( \frac{1}{x}+\frac{1}{y} +\frac{1}{z}\right )](/forum/ext/geomar/texintegr/latexrender/pictures/330f02a4bfceb5e6ba21c8af1652ec5b.png)
 και η ανισότητα γίνεται
και η ανισότητα γίνεται![\displaystyle \frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{r_{a}r_{b}r_{c}}\left ( \frac{1}{r_{a}}+\frac{1}{r_{b}} +\frac{1}{r_{c}}\right ) \displaystyle \frac{r_{a}}{r_{b}}+\frac{r_{b}}{r_{c}}+\frac{r_{c}}{r_{a}}\geq \sqrt[3]{r_{a}r_{b}r_{c}}\left ( \frac{1}{r_{a}}+\frac{1}{r_{b}} +\frac{1}{r_{c}}\right )](/forum/ext/geomar/texintegr/latexrender/pictures/9a6f09c12e989d664f6716528d6e0409.png)
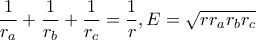 και έτσι προέκυψε η ανισότητα που πρότεινα.
και έτσι προέκυψε η ανισότητα που πρότεινα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης