 διπλώνουμε κατά μήκος της
διπλώνουμε κατά μήκος της 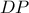 και το
και το  έρχεται στη θέση
έρχεται στη θέση  .
.Οι
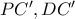 , τέμνουν την
, τέμνουν την  στα σημεία
στα σημεία  . Υπολογίστε το μήκος του
. Υπολογίστε το μήκος του  .
.Προαιρετικό : Μπορούμε να γενικεύσουμε για πλευρά
 και
και 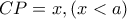 ;
; διπλώνουμε κατά μήκος της
διπλώνουμε κατά μήκος της 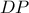 και το
και το  έρχεται στη θέση
έρχεται στη θέση  .
.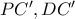 , τέμνουν την
, τέμνουν την  στα σημεία
στα σημεία  . Υπολογίστε το μήκος του
. Υπολογίστε το μήκος του  .
. και
και 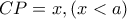 ;
;Έστω
 το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 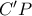 ,
,  ,
,  το σημείο τομής των τμημάτων
το σημείο τομής των τμημάτων 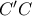 ,
, 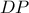 και
και  το σημείο τομής του τμήματος
το σημείο τομής του τμήματος  με την παράλληλης από το
με την παράλληλης από το  προς την
προς την  .
.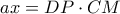 , άρα
, άρα 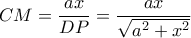
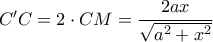
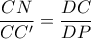 , άρα
, άρα 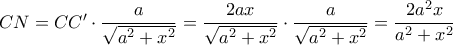
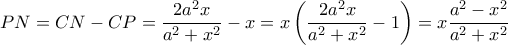
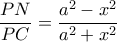
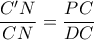 , άρα
, άρα 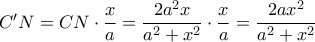 .
.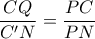 , άρα
, άρα 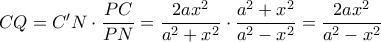 .
.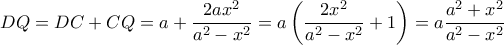 .
.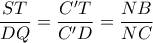 , άρα
, άρα 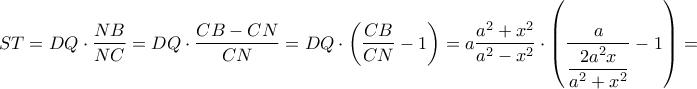
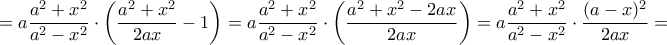
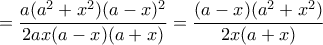
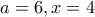 βρίσκουμε
βρίσκουμε 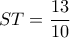 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες