
για κάθε θετικό ακέραιο
 με
με 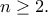
Συντονιστές: achilleas, emouroukos, silouan
Επαγωγικά μπορούμε να δείξουμε ότι το αριστερό μέλος ισούται
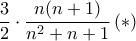 . Πράγματι για
. Πράγματι για  άμεσο.
άμεσο.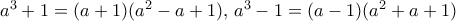 , έχουμε έναν ακόμα παράγοντα, τον
, έχουμε έναν ακόμα παράγοντα, τον 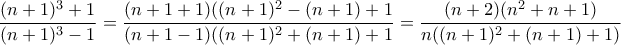 .
.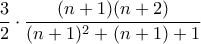 , που είναι ο σωστός επόμενος όρος.
, που είναι ο σωστός επόμενος όρος. είναι
είναι 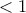 , έπεται το ζητούμενο.
, έπεται το ζητούμενο.Μια λύση που σίγουρα δεν είναι η ενδεδειγμένη, αλλά αναδεικνύει μια όμορφη μέθοδο:
 , η οποία να παίρνει μόνο θετικές τιμές και να είναι τέτοια ώστε
, η οποία να παίρνει μόνο θετικές τιμές και να είναι τέτοια ώστε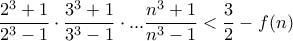
 για να δουλέψει τόσο η βάση της επαγωγής, όσο και το επαγωγικό βήμα.
για να δουλέψει τόσο η βάση της επαγωγής, όσο και το επαγωγικό βήμα.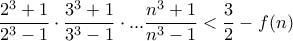
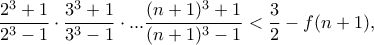
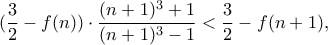
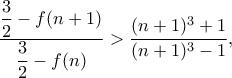
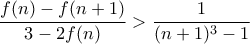
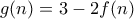 , οπότε, αφού
, οπότε, αφού 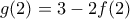 , πρέπει
, πρέπει 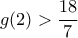 και η πιο πάνω γράφεται
και η πιο πάνω γράφεται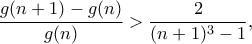
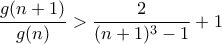
 πρέπει να έχει τις εξής ιδιότητες:
πρέπει να έχει τις εξής ιδιότητες: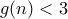 , για κάθε
, για κάθε  (καθώς
(καθώς 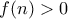 ), και
), και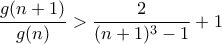
 ώστε
ώστε 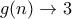 όταν
όταν  . Μια λογική επιλογή είναι η
. Μια λογική επιλογή είναι η 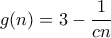 με
με  σταθερά. Αν
σταθερά. Αν  , η
, η  εύκολα ελέγχεται ότι ικανοποιεί την πρώτη ιδιότητα
εύκολα ελέγχεται ότι ικανοποιεί την πρώτη ιδιότητα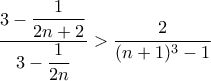 ,
,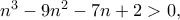
 , ισχύει.
, ισχύει.  , και απλά επαληθεύουμε ότι ισχύει η
, και απλά επαληθεύουμε ότι ισχύει η 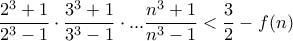
 , όπου
, όπου 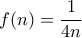 και η
και η 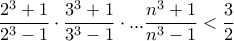
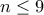 . Σαφώς αρκεί να το δείξουμε για
. Σαφώς αρκεί να το δείξουμε για  . Αυτό είναι εύκολο, οπότε η απόδειξη ολοκληρώθηκε.
. Αυτό είναι εύκολο, οπότε η απόδειξη ολοκληρώθηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες