 και τα ύψη του
και τα ύψη του 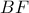 και
και  τέμνονται στο
τέμνονται στο  .
.Οι προεκτάσεις των
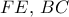 τέμνονται στο
τέμνονται στο  .
.Από το μέσο
 της
της  φέρνω παράλληλη στη διχοτόμο της γωνίας
φέρνω παράλληλη στη διχοτόμο της γωνίας  που τέμνει τις
που τέμνει τις  στα
στα  αντίστοιχα.
αντίστοιχα.Δείξτε ότι οι κύκλοι
 και
και  έχουν ίσες ακτίνες.
έχουν ίσες ακτίνες.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 και τα ύψη του
και τα ύψη του 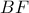 και
και  τέμνονται στο
τέμνονται στο  .
.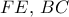 τέμνονται στο
τέμνονται στο  .
. της
της  φέρνω παράλληλη στη διχοτόμο της γωνίας
φέρνω παράλληλη στη διχοτόμο της γωνίας  που τέμνει τις
που τέμνει τις  στα
στα  αντίστοιχα.
αντίστοιχα. και
και  έχουν ίσες ακτίνες.
έχουν ίσες ακτίνες.Ορέστης Λιγνός έγραψε:Δίνεται αμβλυγώνιο τρίγωνοκαι τα ύψη του
και
τέμνονται στο
.Οι προεκτάσεις των
τέμνονται στο
. Από το μέσο
της
φέρνω παράλληλη στη διχοτόμο της γωνίας
που τέμνει τις
στα
αντίστοιχα. Δείξτε ότι οι κύκλοι
και
έχουν ίσες ακτίνες.
 Έστω
Έστω  τα σημεία τομής της διχοτόμου της γωνίας
τα σημεία τομής της διχοτόμου της γωνίας  με τις
με τις  αντίστοιχα.
αντίστοιχα.  είναι προφανώς εγγράψιμα
είναι προφανώς εγγράψιμα  .
.


 ισοσκελές
ισοσκελές  ισοσκελές άρα
ισοσκελές άρα 
 .
. Έστω
Έστω  το σημείο τομής της εκ του
το σημείο τομής της εκ του  παραλλήλου προς την
παραλλήλου προς την  με την
με την  . Τότε με
. Τότε με  το μέσο της
το μέσο της  .
. και από
και από 
 .
.
 .
.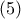 προκύπτοι ότι οι ίσες χορδές
προκύπτοι ότι οι ίσες χορδές  των κύκλων
των κύκλων  «φαίνονται»
«φαίνονται»  αντίστοιχα υπό παραπληρωματικές γωνίες και συνεπώς οι κύκλοι είναι ίσες και το ζητούμενο έχει αποδειχθεί.
αντίστοιχα υπό παραπληρωματικές γωνίες και συνεπώς οι κύκλοι είναι ίσες και το ζητούμενο έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης