Περὶ τοῦ ἀθροίσματος τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου

Γ.-Σ. Σμυρλής · #1

Ἕνα κυρτὸ πολύγωνο βρίσκεται ἐντὸς ἑνὸς μοναδιαίου τετραγώνου. Δείξατε ὅτι τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου δὲν ξεπερνᾶ τὸ 4.

Al.Koutsouridis · #2

Γ.-Σ. Σμυρλής έγραψε:Ἕνα κυρτὸ πολύγωνο βρίσκεται ἐντὸς ἑνὸς μοναδιαίου τετραγώνου. Δείξατε ὅτι τὸ ἄθροισμα τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου δὲν ξεπερνᾶ τὸ 4.

Μια προσπάθεια, όχι και τόσο αυστηρή.

: kurto_polugono_se_tetragwno.png (112.51 KiB) Προβλήθηκε 1043 φορές

'Εστω $A_{1}A_{2}A_{3}A_{4}$ ( $A_{1}A_{2}= a$ κτλ βλ. σχήμα) το μοναδιαίο τετράγωνο και $P_{1}P_{2}...P_{k}$ το κυρτό πολύγωνο στο εσωτερικό του.

Ας είναι $P_{n}$ το σημείο του πολυγώνου πλησιέστερο προς την πάνω πλευρά $A_{1}A_{2}$ ( ένα από τα πολύ δυο τέτοια σημεία, αφού είναι κυρτό). Όμοια $P_{w}, P_{s}, P_{e}$ τα σημεία του πολυγώνου πλησιέστερα προς την δεξιά, κάτω και αριστερή πλευρά του τετραγώνου αντίστοιχα.

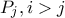Θεωρούμε την διαγώνιο $P_{e}P_{w}$ η οποία χωρίζει το πολύγωνο σε δυο κυρτά πολυγώνα που βρίσκονται σε διαφορετικά ημιεπίπεδα. Θεωρούμε την τεθλασμένη με την φορά των δεικτών του ρολογιού $P_{e}P_{e+1}...P_{w}$ που βρίσκεται πάνω από την διαγώνιο. Λόγω της φύσης της επιλογής των $P_{e}, P_w}$ και της κυρτότητας κάθε σημείο $P_{i}$ της τεθλασμένης θα βρίσκεται δεξιότερα του $P_{j} , i>j$ . Έτσι οι προβολές των πλευρών( έστω $p_{e}, p_{e+1}, ...,p_{w-1}$ ) του πολυγώνου που αντιστοιχούν σε αυτή την τεθλασμένη θα είναι μη επικαλυπτόμενα τμήματα ( $a_{e}, a_{e+1}, ...,a_{w-1}$ ) στην πλευρά $A_{1}A_{2}$ . Και για τα μήκη τους ισχύει

$a_{e}+a_{e+1}+ ...+a_{w-1} = \sum a_{i} \leq 1$ (1) (με

συμβολίζουμε την πλευρά στην οποία κάναμε την προβολή)

Εργαζόμαστε παρόμοια και για την τεθλασμένη κάτω από την διαγώνιο $P_{e}P_{w}$ , καθώς και δεξιά και αριστερά της διαγωνίου $P_{n}P_{s}$ .

Με αυτή την διαδικασία κατά μοναδικό τρόπο αντιστοιχούμε σε κάθε πλευρά του πολυγώνου δυο προβολές σε πλευρές του τετραγώνου για τις οποίες ισχύει $p^{2}_{i} = x^{2}_{i}+y^{2}_{i}$ για κατάλληλα $x \neq y \in \left {a,b,c,d \right }$ . Οπότε θα έχουμε

$\sum p^{2}_{i} = \sum x^{2}_{i} +\sum y^{2}_{i}$ ή αν τα ομαδοποιήσουμε κατάλληλα ανά πλευρά στην οποία προβλήθηκαν.

$\sum p^{2}_{i} = \sum a^{2}_{i} +\sum b^{2}_{i} +\sum c^{2}_{i} +\sum d^{2}_{i}$ λόγω της (1)

$\sum a^{2}_{i} +\sum b^{2}_{i} +\sum c^{2}_{i} +\sum d^{2}_{i} \leq (\sum a_{i})^2 +(\sum b_{i})^2 +(\sum c_{i})^2+(\sum d_{i})^2 \leq 1+1+1+1 =4$

Περὶ τοῦ ἀθροίσματος τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου

Περὶ τοῦ ἀθροίσματος τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου

Re: Περὶ τοῦ ἀθροίσματος τῶν τετραγώνων τῶν πλευρῶν τοῦ πολυγώνου

Μέλη σε σύνδεση