Καλησπέρα.
Στο τρίγωνο
 του παραπάνω σχήματος είναι
του παραπάνω σχήματος είναι  .
.Υπολογίστε το μέτρο της γωνίας
 .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 του παραπάνω σχήματος είναι
του παραπάνω σχήματος είναι  .
. .
.Φανης Θεοφανιδης έγραψε: ↑Παρ Σεπ 21, 2018 9:35 pm10.png
Καλησπέρα.
Στο τρίγωνοτου παραπάνω σχήματος είναι
.
Υπολογίστε το μέτρο της γωνίας.
 έστω σημείο
έστω σημείο  με
με 
 έχουν,
έχουν,  άρα
άρα  και
και  και
και 
 με
με  ,θα είναι
,θα είναι  κι επειδή
κι επειδή 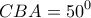
 θα είναι συνευθειακά με
θα είναι συνευθειακά με  και προφανώς
και προφανώς 
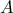 στην
στην  τέμνει την
τέμνει την  στο
στο  ,θα είναι
,θα είναι  ,άρα
,άρα 
 το
το  είναι ισόπλευρο με
είναι ισόπλευρο με  ύψος του
ύψος του
Ανάδρομη κατασκευή.Φανης Θεοφανιδης έγραψε: ↑Παρ Σεπ 21, 2018 9:35 pm10.png
Καλησπέρα.
Στο τρίγωνοτου παραπάνω σχήματος είναι
.
Υπολογίστε το μέτρο της γωνίας.

 και γράφω το περιγεγραμμένο του κύκλο κέντρου
και γράφω το περιγεγραμμένο του κύκλο κέντρου  και ακτίνας, έστω
και ακτίνας, έστω  . Προφανώς το τρίγωνο
. Προφανώς το τρίγωνο  είναι ισόπλευρο.
είναι ισόπλευρο. . Ενώ
. Ενώ 
 τέμνει τη
τέμνει τη  στο
στο  . Γράφω τώρα και το περιγεγραμμένο κύκλο
. Γράφω τώρα και το περιγεγραμμένο κύκλο  που τέμνει ακόμα την
που τέμνει ακόμα την  στο
στο  . Από το εγγεγραμμένο τετράπλευρο
. Από το εγγεγραμμένο τετράπλευρο  με απλό κυνήγι γωνιών προκύπτουν:
με απλό κυνήγι γωνιών προκύπτουν:
 η εξωτερική του γωνία στο
η εξωτερική του γωνία στο  είναι:
είναι:  .
. .
.Καλησπέρα.Φανης Θεοφανιδης έγραψε: ↑Παρ Σεπ 21, 2018 9:35 pm[
Καλησπέρα.
Στο τρίγωνοτου παραπάνω σχήματος είναι
.
Υπολογίστε το μέτρο της γωνίας.
 . Παίρνουμε τώρα σημείο
. Παίρνουμε τώρα σημείο  πάνω στην
πάνω στην  ώστε
ώστε  . Τέλος, παίρνουμε σημείο
. Τέλος, παίρνουμε σημείο  πάνω στην
πάνω στην  ώστε
ώστε  .
. είναι ισοσκελές τραπέζιο, είναι
είναι ισοσκελές τραπέζιο, είναι  και επίσης
και επίσης  .
. είναι ισοσκελές, οπότε
είναι ισοσκελές, οπότε  . Επίσης, από το τρίγωνο
. Επίσης, από το τρίγωνο  , είναι
, είναι  . Επομένως, τα τρίγωνα
. Επομένως, τα τρίγωνα  έχουν
έχουν  , άρα είναι ίσα. Επομένως,
, άρα είναι ίσα. Επομένως,  .
.  και το
και το  ανήκουν στη μεσοκάθετο της
ανήκουν στη μεσοκάθετο της  , οπότε
, οπότε  . Επίσης,
. Επίσης,  .
. , άρα το
, άρα το  είναι ισόπλευρο. Άρα, αφού το
είναι ισόπλευρο. Άρα, αφού το  είναι ισοσκελές τραπέζιο, είναι
είναι ισοσκελές τραπέζιο, είναι  .
. 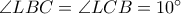 .
. έχουν
έχουν 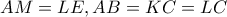 και
και  , άρα είναι ίσα.
, άρα είναι ίσα. .
. έχουν
έχουν  , άρα είναι ίσα και
, άρα είναι ίσα και  .
. , και αφού
, και αφού  .
. .
. σημείο της
σημείο της  ώστε
ώστε  και
και  σημείο στην
σημείο στην  ώστε
ώστε  .
. είναι ισοσκελές.
είναι ισοσκελές. και ακτίνα
και ακτίνα  και έστω πως τέμνει για δεύτερη φορά την
και έστω πως τέμνει για δεύτερη φορά την  στο
στο  .
. , άρα αφού
, άρα αφού  ισχύει ότι
ισχύει ότι 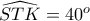 , οπότε η
, οπότε η  είναι η διχοτόμος της
είναι η διχοτόμος της  .
. ως επίκεντρη της
ως επίκεντρη της  είναι διπλάσιά της, οπότε
είναι διπλάσιά της, οπότε  , άρα η
, άρα η 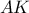 είναι η διχοτόμος της
είναι η διχοτόμος της  .
. και
και  , άρα
, άρα  .
. .
. που ισχύει.
που ισχύει. , άρα από τα παραπάνω
, άρα από τα παραπάνω  .
. .
. και επομένως
και επομένως  και ως αποτέλεσμα
και ως αποτέλεσμα  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης