 ,
,  . Να βρεθεί ο γεωμετρικός τόπος των σημείων
. Να βρεθεί ο γεωμετρικός τόπος των σημείων  του επιπέδου με την ιδιότητα
του επιπέδου με την ιδιότητα  , όπου
, όπου  δοθείς θετικός αριθμός.
δοθείς θετικός αριθμός.Hint:
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 ,
,  . Να βρεθεί ο γεωμετρικός τόπος των σημείων
. Να βρεθεί ο γεωμετρικός τόπος των σημείων  του επιπέδου με την ιδιότητα
του επιπέδου με την ιδιότητα  , όπου
, όπου  δοθείς θετικός αριθμός.
δοθείς θετικός αριθμός.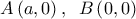 , με
, με  και το μεταβλητό σημείο
και το μεταβλητό σημείο 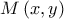 .
.

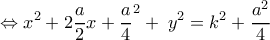

 είναι κύκλος με κέντρο
είναι κύκλος με κέντρο 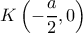 και ακτίνα
και ακτίνα 
 στο επίπεδο, ο γεωμετρικός τόπος του
στο επίπεδο, ο γεωμετρικός τόπος του  είναι ο κύκλος με κέντρο σημείο
είναι ο κύκλος με κέντρο σημείο  ώστε
ώστε  και με ακτίνα
και με ακτίνα  .
. τυχαία σταθερά σημεία στο επίπεδο, και σημείο
τυχαία σταθερά σημεία στο επίπεδο, και σημείο  ώστε
ώστε 

 , σταθερό, οπότε το
, σταθερό, οπότε το  βρίσκεται σε κύκλο με κέντρο το σημείο
βρίσκεται σε κύκλο με κέντρο το σημείο  και με ακτίνα
και με ακτίνα  .
.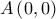 και οριζόντιο άξονα την ευθεία
και οριζόντιο άξονα την ευθεία  , έστω δε
, έστω δε  . Ας είναι και
. Ας είναι και  .
. δίδεται ότι :
δίδεται ότι :  Αλλά ,
Αλλά ,

 γράφεται:
γράφεται:  και παριστάνει
και παριστάνει  κι ακτίνας
κι ακτίνας 
 και προέκυψαν :
και προέκυψαν : 
 στην προς το
στην προς το  προέκταση του
προέκταση του  με
με  .
. ή
ή δηλαδή:
δηλαδή:  .
. είναι σταθερό κι αν
είναι σταθερό κι αν  θα προκύψει:
θα προκύψει: 
 κι ακτίνα ,
κι ακτίνα , 
 , με
, με 
 το μέσον της
το μέσον της  .
. 
 ως προς το
ως προς το  (έστω
(έστω  ).
). 
 κινείται σε σταθερό κύκλο κέντρου
κινείται σε σταθερό κύκλο κέντρου  και ακτίνας
και ακτίνας 
 με
με  μέσον της
μέσον της  .
.
 κινείται σε κύκλο κέντρου
κινείται σε κύκλο κέντρου  και ακτίνας
και ακτίνας  , και τώρα μπορούμε να προσδιορίσουμε την θέση του σημείου
, και τώρα μπορούμε να προσδιορίσουμε την θέση του σημείου  ,το
,το από το
από το  , στην προέκταση της
, στην προέκταση της  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες