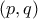 που ικανοποιούν την
που ικανοποιούν την  . Για μαθητές.
. Για μαθητές.Συντονιστές: cretanman, silouan, rek2
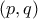 που ικανοποιούν την
που ικανοποιούν την  . Για μαθητές.
. Για μαθητές.
 και αφού η περίπτωση για
και αφού η περίπτωση για  απορρίπτεται, έπεται ότι
απορρίπτεται, έπεται ότι  .
. . Άρα
. Άρα  ή
ή  . Όμως
. Όμως  , άρα έχουμε πως
, άρα έχουμε πως  (1).
(1). 
 (2).
(2). (3), καθώς
(3), καθώς  (αφού
(αφού  πρώτος και
πρώτος και  ).
).


 (4)
(4) .
. άρα
άρα  ή
ή  .
. (βλέποντας πως η εξίσωση
(βλέποντας πως η εξίσωση  δεν έχει λύση στο σύνολο που μας ενδιαφέρει), ενώ στην περίπτωση που
δεν έχει λύση στο σύνολο που μας ενδιαφέρει), ενώ στην περίπτωση που  , η εξίσωση
, η εξίσωση  έχει μοναδική λύση
έχει μοναδική λύση  (στους θετικούς) που εγκρίνεται.
(στους θετικούς) που εγκρίνεται. 
Η εξίσωση γράφεται ισοδύναμαJimNt. έγραψε:Να βρείτε όλα τα ζεύγη πρώτωνπου ικανοποιούν την
. Για μαθητές.
 (1).
(1). .
. , και αφού
, και αφού  πρώτος,
πρώτος,  ή
ή  .
. , άρα
, άρα  , οπότε
, οπότε  , που δεν επαληθεύει.
, που δεν επαληθεύει. , έστω
, έστω  , με
, με  .
. .
. .
. .
. ),
),  .
. , οπότε
, οπότε  , που ισχύει για
, που ισχύει για  .
. ,
,  , με λύση
, με λύση  .
. ,
,  , που δεν έχει λύση.
, που δεν έχει λύση. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες