ΜΚΔ ΚΑΙ ΕΚΠ

[panagiotis iliopoulos]

Έστω θετικοί ακέραιοι. Δείξτε ότι



Έστω και , και με .
Έστω ότι το ζητούμενο ισχύει. Έχουμε 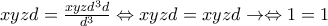(που ισχύει, άρα ισχύει το ζητούμενο).

[Mihalis_Lambrou]

Έστω θετικοί ακέραιοι. Δείξτε ότι



Έστω και , και με .
Έστω ότι το ζητούμενο ισχύει. Έχουμε 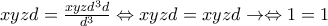(που ισχύει, άρα ισχύει το ζητούμενο).

Παναγιώτη, για ξαναδές το αυτό.

Για παράδειγμα στον παρονομαστή έχεις πάρει .

Όμως για έχουμε 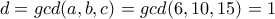αλλά δεν ισχύει αφού .

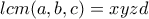Ας προσθέσω ότι ούτε ο ισχυρισμός είναι σωστός.

[Demetres]

Ας δούμε μια απόδειξη.

Θα δείξω ότι



όπου με παρενθέσεις συμβολίζω τον μέγιστο κοινό διαιρέτη και με αγκύλες το ελάχιστο κοινό πολλαπλάσιο.

Αρκεί για κάθε πρώτο να δείξω ότι η μέγιστη δύναμη του που διαιρεί το αριστερό μέλος, ισούται με την μέγιστη δύναμη του που διαιρεί και το δεξί μέλος.

Ας υποθέσουμε ότι οι μέγιστες δυνάμεις του που διαιρούν τα είναι αντίστοιχα. Χωρίς βλάβη της γενικότητας είναι . Τότε:

Η μέγιστη δύναμη του που διαιρεί το ισούται με .
Η μέγιστη δύναμη του που διαιρεί το ισούται με .
Η μέγιστη δύναμη του που διαιρεί το ισούται με .
Η μέγιστη δύναμη του που διαιρεί το ισούται με .
Η μέγιστη δύναμη του που διαιρεί το ισούται με .

Άρα η μέγιστη δύναμη του που διαιρεί το αριστερό μέλος ισούται με και
η μέγιστη δύναμη του που διαιρεί το δεξί μέλος ισούται με .

Οπότε το ζητούμενο αποδείχθηκε.