 ένας περιττός πρώτος.
ένας περιττός πρώτος. Έστω, επίσης,
 , με το κλάσμα
, με το κλάσμα  ανάγωγο.
ανάγωγο.Να δείξετε ότι
 .
.Συντονιστές: cretanman, silouan, rek2
 ένας περιττός πρώτος.
ένας περιττός πρώτος.  , με το κλάσμα
, με το κλάσμα  ανάγωγο.
ανάγωγο. .
.Δεν νομίζω ότι χρειάζεται το Θ.Wilson.ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Τετ Απρ 03, 2019 8:02 pmΚαλησπέρα!
Παρατηρούμε ότι
άρα από το θεώρημαείναι
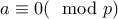




Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες