 ώστε
ώστε 
Συντονιστές: cretanman, silouan, rek2
Έχουμε,ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Κυρ Φεβ 09, 2020 10:49 pmΝα προσδιορίσετε όλους του μη αρνητικούς ακεραίουςώστε

 . Οπότε,
. Οπότε,  και
και  με
με  μη αρνητικούς ακέραιους.
μη αρνητικούς ακέραιους. , τότε
, τότε  , άτοπο.
, άτοπο. , τότε ομοίως προκύπτει
, τότε ομοίως προκύπτει  , άτοπο.
, άτοπο.
 και
και  . Τότε,
. Τότε,  .
.
 και
και  . Τότε,
. Τότε,  .
. έχουμε ότι
έχουμε ότι  και
και  , άτοπο.
, άτοπο. , τότε
, τότε  , άτοπο.
, άτοπο. 
 και
και  . Τότε,
. Τότε,  , άτοπο.
, άτοπο.
 και
και  . Τότε,
. Τότε,  , οπότε
, οπότε  .
. , έχουμε
, έχουμε  . Ακόμη
. Ακόμη  , που δίνει
, που δίνει  με
με  φυσικό.
φυσικό. οπότε
οπότε  με
με  φυσικό.
φυσικό. , έχουμε
, έχουμε  , ή
, ή  οπότε παίρνουμε τις λύσεις
οπότε παίρνουμε τις λύσεις  που εύκολα απορρίπτονται.
που εύκολα απορρίπτονται. , τότε
, τότε  και προκύπτει
και προκύπτει  .
. .
. (γιατί;) .Άρα η αρχική εξίσωση γίνεται:
(γιατί;) .Άρα η αρχική εξίσωση γίνεται:

 ,
, .Από δω και πέρα εύκολα.....
.Από δω και πέρα εύκολα..... τέτοιοι ώστε:
τέτοιοι ώστε: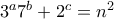
 έχουμε την :
έχουμε την :

 τότε:
τότε: έχω
έχω  και έτσι έχω:
και έτσι έχω:
 έχουμε της ακόλουθες
έχουμε της ακόλουθες  περίπτωσης
περίπτωσης και
και  που είναι προφανές πως είναι αδύνατο
που είναι προφανές πως είναι αδύνατο και
και 
 και
και 
 έχω
έχω  δηλαδή πρέπει
δηλαδή πρέπει 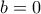 οπότε λύνουμε την:
οπότε λύνουμε την: που είναι γνωστή .1)Με
που είναι γνωστή .1)Με  τελιωνη εύκολα.2)Αν
τελιωνη εύκολα.2)Αν  ,Αν
,Αν  με
με  έχω
έχω  και αφερεση τετραγώνων......
και αφερεση τετραγώνων......
 και
και  ισοδύναμα
ισοδύναμα  και
και 
 έχουμε
έχουμε  . Διακρίνουμε τίς περίπτωσης:
. Διακρίνουμε τίς περίπτωσης: Αν
Αν έχουμε την:
έχουμε την:  που έχει λύση την
που έχει λύση την .Αν
.Αν  τότε την γράφουμε στην μορφή:
τότε την γράφουμε στην μορφή:



 έχουμε της λυση :
έχουμε της λυση :

 τότε με
τότε με  έχω
έχω  ,
, :
: .
.  έχω της ακόλουθες
έχω της ακόλουθες περιπτώσεις:
περιπτώσεις:
 και
και  που είναι αδύνατη αφού
που είναι αδύνατη αφού

 και
και  ισοδύναμα
ισοδύναμα  και
και 
 περνοντας
περνοντας  έχω
έχω
 αλλά τότε δεν ισχύει η
αλλά τότε δεν ισχύει η 
 και
και  ισοδύναμα
ισοδύναμα  και
και 
 έχω
έχω  . Διακρίνουμε
. Διακρίνουμε  περίπτωσης:
περίπτωσης: Αν
Αν  έχουμε:
έχουμε: 
 Αν
Αν 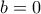 έχω
έχω 
 με
με  έχω
έχω 

 Αν
Αν  έχω
έχω  αντίστοιχα.
αντίστοιχα. τότε :
τότε :
 έχω:
έχω:
 έχω :
έχω :


 Αν
Αν
 έχω
έχω  και
και  και μετατρέπεται στην:
και μετατρέπεται στην:
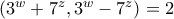 έχω της ακόλουθες
έχω της ακόλουθες  περίπτωσης
περίπτωσης Αν
Αν  και
και  που είναι προφανές αδύνατη
που είναι προφανές αδύνατη Αν
Αν  και
και 
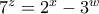 και
και 

 δεινή τής λύσης:
δεινή τής λύσης:

Μέλη σε αυτήν τη Δ. Συζήτηση: Aba και 6 επισκέπτες