Θεωρία αριθμών
Δημοσιεύτηκε: Σάβ Ιαν 30, 2021 8:38 pm
Να βρεθούν όλοι οι  τέτοιοι ώστε:
τέτοιοι ώστε:

 τέτοιοι ώστε:
τέτοιοι ώστε:
https://www.mathematica.gr/forum/
https://www.mathematica.gr/forum/viewtopic.php?f=175&t=68935
 τέτοιοι ώστε:
τέτοιοι ώστε:
Μία λύση είναι η
 και
και  οτιδήποτε, οπότε μπορούμε να υποθέσουμε
οτιδήποτε, οπότε μπορούμε να υποθέσουμε  .
. ) γράφεται
) γράφεται 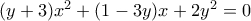 .
.  έχει διακρίνουσα
έχει διακρίνουσα  . Άρα
. Άρα  (όπου βέβαια
(όπου βέβαια  περιττός) και άρα
περιττός) και άρα 
 που βρήκαμε, δηλαδή
που βρήκαμε, δηλαδή  θα βρούμε (ελπίζω να έκανα σωστά τις πράξεις)
θα βρούμε (ελπίζω να έκανα σωστά τις πράξεις) 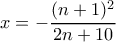 και
και 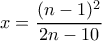 (είναι ίδιες με
(είναι ίδιες με  στην θέση του
στην θέση του  ). Κρατάμε χωρίς βλάβη την πρώτη. Άρα
). Κρατάμε χωρίς βλάβη την πρώτη. Άρα  από όπου
από όπου  , και λοιπά. Τα υπόλοιπα απλό συμμάζεμα.
, και λοιπά. Τα υπόλοιπα απλό συμμάζεμα. βρήκα λύσεις τις α)
βρήκα λύσεις τις α)  που προκύπτει από την
που προκύπτει από την  , β)
, β)  που προκύπτει από την
που προκύπτει από την 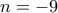 , γ)
, γ)  που προκύπτει από την
που προκύπτει από την  και δ)
και δ) 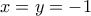 από την
από την  . Έκανα και έλεγχο στην αρχική, και επαληθεύουν.
. Έκανα και έλεγχο στην αρχική, και επαληθεύουν. τότε
τότε  .
. .......
.......Την έχω υπόψη και αυτή την λύση. Επειδή έχει παρόμοιο πλήθος πράξεων, τουλάχιστον όπως το έκανα, έγραψα μόνο την μία λύση.
 , άρα
, άρα  . Έπεται
. Έπεται  και συγχρόνως
και συγχρόνως  . Εξετάζουμε τώρα τα
. Εξετάζουμε τώρα τα  αυτά ζεύγη και με προσθεφαίρεση βρίσκουμε τα
αυτά ζεύγη και με προσθεφαίρεση βρίσκουμε τα  και από εκεί τα
και από εκεί τα  .
.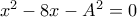 οπότε η διακρίνουσα πρέπει να είναι τέλειο τετράγωνο, εδώ
οπότε η διακρίνουσα πρέπει να είναι τέλειο τετράγωνο, εδώ  . Άρα
. Άρα  , οπότε
, οπότε και όπως πριν έχουμε
και όπως πριν έχουμε  ίσον οι διαιρέτες του
ίσον οι διαιρέτες του 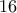 , και λοιπά.
, και λοιπά.