
να ισούται με τη δύναμη κάποιου πρώτου αριθμού.
Συντονιστές: cretanman, silouan, rek2

 . Τότε κάθε ένα εκ των
. Τότε κάθε ένα εκ των  είναι δύναμη του
είναι δύναμη του  . Έστω
. Έστω  . Δηλαδή ισχύει ότι
. Δηλαδή ισχύει ότι  με
με  θετικούς ακεραίους με τουλάχιστον ένα να μην είναι πολλαπλάσιος του
θετικούς ακεραίους με τουλάχιστον ένα να μην είναι πολλαπλάσιος του  .
.  είναι επίσης δυνάμεις του
είναι επίσης δυνάμεις του  , και άρα και πολλαπλάσια του
, και άρα και πολλαπλάσια του  αφού δεν μπορούν να ισούνται με
αφού δεν μπορούν να ισούνται με  . Τότε έχω
. Τότε έχω  από το οποίο παίρνω
από το οποίο παίρνω  . Ομοίως παίρνω
. Ομοίως παίρνω  και
και  . Αφού όμως τα
. Αφού όμως τα  δεν είναι όλα πολλαπλάσια του
δεν είναι όλα πολλαπλάσια του  τότε πρέπει
τότε πρέπει  .
.  είναι όλα μεγαλύτερα ή ίσα του
είναι όλα μεγαλύτερα ή ίσα του 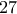 (και άρα πολλαπλάσια του
(και άρα πολλαπλάσια του 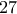 ) θα έχω
) θα έχω  . Δηλαδή
. Δηλαδή  . Ομοίως παίρνω
. Ομοίως παίρνω  και
και  που είναι άτοπο.
που είναι άτοπο. είναι ίσο με
είναι ίσο με  ή
ή  .
.  τότε
τότε  και έχω
και έχω  και
και  . Τότε
. Τότε  . Εύκολα καταλήγουμε σε
. Εύκολα καταλήγουμε σε  και
και  . Έχουμε λοιπόν την τριάδα
. Έχουμε λοιπόν την τριάδα  που δίνει ως λύσεις τις τριάδες
που δίνει ως λύσεις τις τριάδες  με
με  μη αρνητικό ακέραιο.
μη αρνητικό ακέραιο. τότε έχουμε να εξετάσουμε τις περιπτώσεις
τότε έχουμε να εξετάσουμε τις περιπτώσεις  . Οι
. Οι  και
και  απορρίπτονται αφού τότε το
απορρίπτονται αφού τότε το  θα ήταν πολλαπλάσιο του
θα ήταν πολλαπλάσιο του  , άτοπο.
, άτοπο.  τότε
τότε  και
και  που δίνει
που δίνει  . Καταλήγουμε σε
. Καταλήγουμε σε  και
και  που είναι άτοπο. (Αφού ένα εκ των
που είναι άτοπο. (Αφού ένα εκ των  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  .)
.) τότε
τότε  και
και  που δίνει
που δίνει  . Καταλήγουμε σε
. Καταλήγουμε σε  και
και  . Έχουμε λοιπόν την τριάδα
. Έχουμε λοιπόν την τριάδα  που δίνει ως λύσεις τις τριάδες
που δίνει ως λύσεις τις τριάδες  με
με  μη αρνητικό ακέραιο. Μαζί με αυτές έχουμε ασφαλώς και όλες τις κυκλικές μεταθέσεις τους.
μη αρνητικό ακέραιο. Μαζί με αυτές έχουμε ασφαλώς και όλες τις κυκλικές μεταθέσεις τους.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης