Προχωρούμε σε τομές
Δημοσιεύτηκε: Σάβ Απρ 01, 2017 8:12 am
Έστω  υποσύνολα του
υποσύνολα του  , ανά δύο διαφορετικά.
, ανά δύο διαφορετικά.
Να βρεθεί η μέγιστη τιμή του , με την υπόθεση
, με την υπόθεση  .
.
( είναι ο αριθμός των στοιχείων του
είναι ο αριθμός των στοιχείων του  ).
).
(Κολομβία 2011)
 υποσύνολα του
υποσύνολα του  , ανά δύο διαφορετικά.
, ανά δύο διαφορετικά. Να βρεθεί η μέγιστη τιμή του
 , με την υπόθεση
, με την υπόθεση  .
. (
 είναι ο αριθμός των στοιχείων του
είναι ο αριθμός των στοιχείων του  ).
).(Κολομβία 2011)
 έχουμε
έχουμε 
 και έστω χωρίς βλάβη της γενικότητας ότι
και έστω χωρίς βλάβη της γενικότητας ότι  . Αν
. Αν  το αποτέλεσμα είναι άμεσο. Το ίδιο και αν
το αποτέλεσμα είναι άμεσο. Το ίδιο και αν 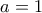 αφού η συνθήκη ότι τα
αφού η συνθήκη ότι τα  . Πρέπει λοιπόν
. Πρέπει λοιπόν  . Τότε όμως είναι
. Τότε όμως είναι  οπότε
οπότε 
 . Η ισότητα λαμβάνεται αν επιλέξουμε τα σύνολα
. Η ισότητα λαμβάνεται αν επιλέξουμε τα σύνολα  .
.