 μήλα,
μήλα,  αχλάδια και
αχλάδια και  πορτοκάλια. Με πόσους τρόπους μπορούμε να δώσουμε
πορτοκάλια. Με πόσους τρόπους μπορούμε να δώσουμε  φρούτα σε
φρούτα σε  παιδιά; (Έχει σημασία το είδος φρούτου) Για μαθητές.
παιδιά; (Έχει σημασία το είδος φρούτου) Για μαθητές.Συντονιστές: Demetres, socrates, silouan
 μήλα,
μήλα,  αχλάδια και
αχλάδια και  πορτοκάλια. Με πόσους τρόπους μπορούμε να δώσουμε
πορτοκάλια. Με πόσους τρόπους μπορούμε να δώσουμε  φρούτα σε
φρούτα σε  παιδιά; (Έχει σημασία το είδος φρούτου) Για μαθητές.
παιδιά; (Έχει σημασία το είδος φρούτου) Για μαθητές. φρούτα στο κάθε παιδί ξεχωριστά ή συνολικά;
φρούτα στο κάθε παιδί ξεχωριστά ή συνολικά;Συνολικά.Διονύσιος Αδαμόπουλος έγραψε:Δίνουμεφρούτα στο κάθε παιδί ξεχωριστά ή συνολικά;
 είναι το πλήθος των μήλων που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα,
είναι το πλήθος των μήλων που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα,  είναι το πλήθος των αχλαδιών που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα και
είναι το πλήθος των αχλαδιών που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα και  πλήθος των πορτοκαλιών που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα.
πλήθος των πορτοκαλιών που θα πάρει το πρώτο και δεύτερο παιδί αντίστοιχα. , με την προϋπόθεση πως
, με την προϋπόθεση πως  .
.  μη αρνητικές λύσεις. Θα αφαιρέσουμε τις άκυρες:
μη αρνητικές λύσεις. Θα αφαιρέσουμε τις άκυρες: , με την προϋπόθεση πως
, με την προϋπόθεση πως  (1).
(1). τότε το πλήθος λύσεων είναι ίσο με το γινόμενο του πλήθους των μη αρνητικών λύσεων της εξίσωσης
τότε το πλήθος λύσεων είναι ίσο με το γινόμενο του πλήθους των μη αρνητικών λύσεων της εξίσωσης  με το πλήθος των μη αρνητικών λύσεων της
με το πλήθος των μη αρνητικών λύσεων της  , δηλαδή
, δηλαδή  .
. έχουμε
έχουμε  λύσεις και αν
λύσεις και αν  έχουμε
έχουμε  λύσεις.
λύσεις. .
. , με
, με  και της
και της  , με
, με  είναι
είναι  και
και  .
.  ,
,  και
και  , έχουμε με PIE πως το πλήθος λύσεων της αρχικής εξίσωσης είναι:
, έχουμε με PIE πως το πλήθος λύσεων της αρχικής εξίσωσης είναι:
 αφού για
αφού για  υπάρχουν
υπάρχουν  τρόποι να δώσουμε
τρόποι να δώσουμε  μήλα στα δύο παιδιά.
μήλα στα δύο παιδιά.
 στην δυναμοσειρά του
στην δυναμοσειρά του 

 όπου όλες οι δυνάμεις που εμφανίζονται στο
όπου όλες οι δυνάμεις που εμφανίζονται στο  είναι μεγαλύτερες του
είναι μεγαλύτερες του  .
.  στο ανάπτυγμα του
στο ανάπτυγμα του 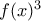 ισούται με
ισούται με
Σας ευχαριστώ πολυ !Demetres έγραψε:Υπάρχει αλλά όχι τόσο απλή:
Η γεννήτρια συνάρτηση της κατανομής των μήλων είναι ηαφού για
υπάρχουν
τρόποι να δώσουμε
μήλα στα δύο παιδιά.
Παρατηρούμε επίσης ότι
Μας ενδιαφέρει ο συντελεστής τουστην δυναμοσειρά του
Από το διωνυμικό θεώρημα είναι
Επίσηςόπου όλες οι δυνάμεις που εμφανίζονται στο
είναι μεγαλύτερες του
.
Άρα ο συντελεστής τουστο ανάπτυγμα του
ισούται με
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης