Ενδιαφέρουσα διάλεξη
Συντονιστές: Demetres, socrates, silouan
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Ενδιαφέρουσα διάλεξη
Κατά τη διάρκεια μιας διάλεξης, καθένας από τους 5 επιστήμονες κοιμήθηκε ακριβώς 2 φορές.
Για κάθε ζευγάρι επιστημόνων, υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα.
Αποδείξτε ότι, κάποια στιγμή, υπήρχαν 3 επιστήμονες που κοιμόντουσαν ταυτόχρονα.
Για κάθε ζευγάρι επιστημόνων, υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα.
Αποδείξτε ότι, κάποια στιγμή, υπήρχαν 3 επιστήμονες που κοιμόντουσαν ταυτόχρονα.
Θανάσης Κοντογεώργης
Λέξεις Κλειδιά:
Re: Ενδιαφέρουσα διάλεξη
Έστω ![A_n =[x_n,y_n]\cup[a_n,b_n] A_n =[x_n,y_n]\cup[a_n,b_n]](/forum/ext/geomar/texintegr/latexrender/pictures/ea04a42d3e2ca902dd95cc295980851a.png) ώστε το
ώστε το  να είναι το χρονικό διάστημα που ο
να είναι το χρονικό διάστημα που ο  επιστήμονας κοιμήθηκε.
επιστήμονας κοιμήθηκε. .
.
Πρέπει να δείξουμε ότι υπάρχουν διακεκριμένα ώστε
διακεκριμένα ώστε  .
.
Βάζουμε τα σύνολα στη σειρά ώστε αν και μόνο αν
αν και μόνο αν  .
.
Αν το σύνολο είναι κενό ορίζουμε
είναι κενό ορίζουμε  .
.
Αν δύο σύνολα τότε
δύο σύνολα τότε  και
και  ώστε
ώστε  συνεπάγεται
συνεπάγεται  .
.
Έχουμε .
.
Τότε έχουμε το οποίο δίνει ότι
το οποίο δίνει ότι 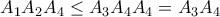 , το οποίο είναι άτοπο αφού το
, το οποίο είναι άτοπο αφού το  δεν είναι κενό από υπόθεση.
δεν είναι κενό από υπόθεση.
Σημείωση: Η παραπάνω απόδειξη δείχνει ότι το αποτέλεσμα ισχύει αν ο αριθμός των επιστημόνων είναι μεγαλύτερος η ίσος του 4.
![A_n =[x_n,y_n]\cup[a_n,b_n] A_n =[x_n,y_n]\cup[a_n,b_n]](/forum/ext/geomar/texintegr/latexrender/pictures/ea04a42d3e2ca902dd95cc295980851a.png) ώστε το
ώστε το  να είναι το χρονικό διάστημα που ο
να είναι το χρονικό διάστημα που ο  επιστήμονας κοιμήθηκε.
επιστήμονας κοιμήθηκε. .
.Πρέπει να δείξουμε ότι υπάρχουν
 διακεκριμένα ώστε
διακεκριμένα ώστε  .
.Βάζουμε τα σύνολα στη σειρά ώστε
 αν και μόνο αν
αν και μόνο αν  .
.Αν το σύνολο
 είναι κενό ορίζουμε
είναι κενό ορίζουμε  .
.Αν
 δύο σύνολα τότε
δύο σύνολα τότε  και
και  ώστε
ώστε  συνεπάγεται
συνεπάγεται  .
.Έχουμε
 .
.Τότε έχουμε
 το οποίο δίνει ότι
το οποίο δίνει ότι 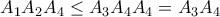 , το οποίο είναι άτοπο αφού το
, το οποίο είναι άτοπο αφού το  δεν είναι κενό από υπόθεση.
δεν είναι κενό από υπόθεση.Σημείωση: Η παραπάνω απόδειξη δείχνει ότι το αποτέλεσμα ισχύει αν ο αριθμός των επιστημόνων είναι μεγαλύτερος η ίσος του 4.
τελευταία επεξεργασία από stranger σε Δευ Αύγ 31, 2020 4:03 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Κωνσταντίνος Σμπώκος
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ενδιαφέρουσα διάλεξη
γιαstranger έγραψε: ↑Δευ Αύγ 31, 2020 12:35 pmΈστωώστε το
να είναι το χρονικό διάστημα που ο
επιστήμονας κοιμήθηκε.
.
Πρέπει να δείξουμε ότι υπάρχουνδιακεκριμένα ώστε
.
Βάζουμε τα σύνολα στη σειρά ώστεαν και μόνο αν
.
Αν το σύνολοείναι κενό ορίζουμε
.
Ανδύο σύνολα τότε
και
ώστε
και
συνεπάγεται
.
Έστω ότι για κάθεδιακεκριμμένα
.
Έχουμε ότι.
Άρα.
Όμως το σύνολοείναι μη κενό από υπόθεση, το οποίο φέρνει το άτοπο και το συμπέρασμα έπεται.
Σημείωση: Η παραπάνω απόδειξη δείχνει ότι το αποτέλεσμα ισχύει αν ο αριθμός των επιστημόνων είναι μεγαλύτερος η ίσος του 3.
 δεν ισχύει.
δεν ισχύει.Πάρε
ο πρώτος να κοιμήθηκε στο
![[1,2]\cup [4,5] [1,2]\cup [4,5]](/forum/ext/geomar/texintegr/latexrender/pictures/5b692a8052ce0a22d219d83500940b43.png)
ο δεύτερος να κοιμήθηκε στο
![[2,3]\cup [7,8] [2,3]\cup [7,8]](/forum/ext/geomar/texintegr/latexrender/pictures/12eba321af459b32f6d3d7ca39df1d71.png)
και ο τρίτος να κοιμήθηκε στο
![[0,1]\cup [8,9] [0,1]\cup [8,9]](/forum/ext/geomar/texintegr/latexrender/pictures/4beba4411970848303ea89f588e29948.png)
Re: Ενδιαφέρουσα διάλεξη
Σταύρο σε ευχαριστώ. Την διόρθωσα την απόδειξή μου (δες παραπάνω). Πρέπει να έχουμε ότι ο αριθμός των επιστηνόνων να είναι μεγαλύτερος η ίσος του 4.
Κωνσταντίνος Σμπώκος
-
Μάρκος Βασίλης
- Δημοσιεύσεις: 303
- Εγγραφή: Σάβ Αύγ 31, 2019 5:47 pm
- Τοποθεσία: Καισαριανή
- Επικοινωνία:
Re: Ενδιαφέρουσα διάλεξη
Το πρόβλημα μπορεί να επανδιατυπωθεί ως εξής: παίρνουμε 5 σπίρτα,  , και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.
, και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.
Αρχικά, παίρνουμε το σπίρτο το οποίο, από υπόθεση θα τέμνει το σπίρτο
το οποίο, από υπόθεση θα τέμνει το σπίρτο  . Στη συνέχεια, παίρνουμε το σπίρτο
. Στη συνέχεια, παίρνουμε το σπίρτο  . Αυτό θα τέμνει και τα δύο άλλα σπίρτα σε κάποια άκρη τους. Αν αυτή είναι η κοινή άκρη των
. Αυτό θα τέμνει και τα δύο άλλα σπίρτα σε κάποια άκρη τους. Αν αυτή είναι η κοινή άκρη των  τότε η απόδειξη καταλήγει. Ειδάλλως, τα τρία σπίρτα θα σχηματίζουν ένα τρίγωνο. Τώρα, παίρνουμε το σπίρτο
τότε η απόδειξη καταλήγει. Ειδάλλως, τα τρία σπίρτα θα σχηματίζουν ένα τρίγωνο. Τώρα, παίρνουμε το σπίρτο  το οποίο θα πρέπει να τέμνει το σπίρτο
το οποίο θα πρέπει να τέμνει το σπίρτο  σε κάποιο από τα άκρα του, συνεπώς θα τέμνει είτε το
σε κάποιο από τα άκρα του, συνεπώς θα τέμνει είτε το  είτε το
είτε το  και η απόδειξη καταλήγει.
και η απόδειξη καταλήγει.
 , και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.
, και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.Αρχικά, παίρνουμε το σπίρτο
 το οποίο, από υπόθεση θα τέμνει το σπίρτο
το οποίο, από υπόθεση θα τέμνει το σπίρτο  . Στη συνέχεια, παίρνουμε το σπίρτο
. Στη συνέχεια, παίρνουμε το σπίρτο  . Αυτό θα τέμνει και τα δύο άλλα σπίρτα σε κάποια άκρη τους. Αν αυτή είναι η κοινή άκρη των
. Αυτό θα τέμνει και τα δύο άλλα σπίρτα σε κάποια άκρη τους. Αν αυτή είναι η κοινή άκρη των  τότε η απόδειξη καταλήγει. Ειδάλλως, τα τρία σπίρτα θα σχηματίζουν ένα τρίγωνο. Τώρα, παίρνουμε το σπίρτο
τότε η απόδειξη καταλήγει. Ειδάλλως, τα τρία σπίρτα θα σχηματίζουν ένα τρίγωνο. Τώρα, παίρνουμε το σπίρτο  το οποίο θα πρέπει να τέμνει το σπίρτο
το οποίο θα πρέπει να τέμνει το σπίρτο  σε κάποιο από τα άκρα του, συνεπώς θα τέμνει είτε το
σε κάποιο από τα άκρα του, συνεπώς θα τέμνει είτε το  είτε το
είτε το  και η απόδειξη καταλήγει.
και η απόδειξη καταλήγει.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ενδιαφέρουσα διάλεξη
Μάρκος Βασίλης έγραψε: ↑Δευ Αύγ 31, 2020 4:13 pmΤο πρόβλημα μπορεί να επανδιατυπωθεί ως εξής: παίρνουμε 5 σπίρτα,, και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.
Αρχικά, παίρνουμε το σπίρτοτο οποίο, από υπόθεση θα τέμνει το σπίρτο
. Στη συνέχεια, παίρνουμε το σπίρτο
. Αυτό θα τέμνει και τα δύο άλλα σπίρτα σε κάποια άκρη τους. Αν αυτή είναι η κοινή άκρη των
τότε η απόδειξη καταλήγει. Ειδάλλως, τα τρία σπίρτα θα σχηματίζουν ένα τρίγωνο. Τώρα, παίρνουμε το σπίρτο
το οποίο θα πρέπει να τέμνει το σπίρτο
σε κάποιο από τα άκρα του, συνεπώς θα τέμνει είτε το
είτε το
και η απόδειξη καταλήγει.
Δεν είναι έτσι γιατί κοιμούνται δύο φορές.Μάρκος Βασίλης έγραψε: ↑Δευ Αύγ 31, 2020 4:13 pmΤο πρόβλημα μπορεί να επανδιατυπωθεί ως εξής: παίρνουμε 5 σπίρτα,, και τα τοποθετούμε έτσι ώστε ανά δύο να τέμνονται σε κάποιο από τα άκρα τους. Θα δείξουμε ότι υπάρχει τριάδα σπίρτων που να τέμνονται.
Αρα ο καθένας θα έπρεπε να αντιστοιχεί σε δύο σπίρτα και τα σπίρτα πάνω σε μια ευθεία κλπ.
Αν κάνω λάθος διορθωσε με .
Υπάρχει ενα σημείο στο πρόβλημα που δεν είναι καθαρό τουλάχιστον για μένα.
Οταν λέει
υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα
θεωρώ ότι εννοεί τουλάχιστον μια.
Δηλαδή θα μπορούσαν να κοιμόντουσαν ταυτόχρονα για ένα διάστημα.
Εσύ θεωρείς ότι
Οταν λέει
υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα
εννοεί ακριβώς μία.
-
Μάρκος Βασίλης
- Δημοσιεύσεις: 303
- Εγγραφή: Σάβ Αύγ 31, 2019 5:47 pm
- Τοποθεσία: Καισαριανή
- Επικοινωνία:
Re: Ενδιαφέρουσα διάλεξη
Εγώ σκέφτηκα ότι ένας επιστήμονας αντιστοιχεί σε ένα σπίρτο και τα δύο άκρα του σπίρτου είναι οι δύο «ύπνοι» του επιστήμονα, οπότε και μετράει η θέση στην οποία τέμνονται.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Αύγ 31, 2020 9:18 pmΔεν είναι έτσι γιατί κοιμούνται δύο φορές.
Αρα ο καθένας θα έπρεπε να αντιστοιχεί σε δύο σπίρτα και τα σπίρτα πάνω σε μια ευθεία κλπ.
Αν κάνω λάθος διορθωσε με .
Υπάρχει ενα σημείο στο πρόβλημα που δεν είναι καθαρό τουλάχιστον για μένα.
Οταν λέει
υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα
θεωρώ ότι εννοεί τουλάχιστον μια.
Δηλαδή θα μπορούσαν να κοιμόντουσαν ταυτόχρονα για ένα διάστημα.
Εσύ θεωρείς ότι
Οταν λέει
υπήρχε μια στιγμή που και οι δύο κοιμόντουσαν ταυτόχρονα
εννοεί ακριβώς μία.
Σε σχέση, τώρα, με την ύπαρξη, πράγματι το αντιμετωπίσαμε διαφορετικά.

Re: Ενδιαφέρουσα διάλεξη
To ποστ μου νούμερο 2 είναι λανθασμένο. Ευχαριστώ το Σταύρο για την επισήμανση.
Ας κάνω άλλη μια προσπάθεια.Έστω ότι δεν υπάρχει στιγμή που να κοιμήθηκαν τρεις επιστήμονες μαζί.
Παρατηρούμε ότι τα σύνολα![A_n = [x_n,y_n] \cup [a_n,b_n] A_n = [x_n,y_n] \cup [a_n,b_n]](/forum/ext/geomar/texintegr/latexrender/pictures/c8d73f28df55b0fa999144170a3d0b69.png) καθώς και οι ενώσεις τους η οι τομές τους τέμνονται αν και μόνο αν τέμνονται σε κάποιο άκρο τους. Άρα μπορούμε να ταυτίσουμε ένα τέτοιο σύνολο με τα άκρα τους.
καθώς και οι ενώσεις τους η οι τομές τους τέμνονται αν και μόνο αν τέμνονται σε κάποιο άκρο τους. Άρα μπορούμε να ταυτίσουμε ένα τέτοιο σύνολο με τα άκρα τους.
Χρησιμοποιώντας την αρχή εγκλεισμού- αποκλεισμού έχουμε
 .
.
Αν τότε
τότε  .
.
Επίσης έχουμε αν τότε
τότε  επειδή κάθε ζεύγος συνόλων τέμνονται από υπόθεση.
επειδή κάθε ζεύγος συνόλων τέμνονται από υπόθεση.
Επίσης από υπόθεση, αν τότε
τότε  .
.
Επίσης το πλήθος των υποσυνόλων του που περιέχουν δύο στοιχεία είναι
που περιέχουν δύο στοιχεία είναι  =
=  .
.
Άρα .
.
Νομίζω από αυτό μπορούμε να πάρουμε άτοπο. Δεν είμαι σίγουρος. Ας την συνεχίσει κάποιος άλλος.
Ας κάνω άλλη μια προσπάθεια.Έστω ότι δεν υπάρχει στιγμή που να κοιμήθηκαν τρεις επιστήμονες μαζί.
Παρατηρούμε ότι τα σύνολα
![A_n = [x_n,y_n] \cup [a_n,b_n] A_n = [x_n,y_n] \cup [a_n,b_n]](/forum/ext/geomar/texintegr/latexrender/pictures/c8d73f28df55b0fa999144170a3d0b69.png) καθώς και οι ενώσεις τους η οι τομές τους τέμνονται αν και μόνο αν τέμνονται σε κάποιο άκρο τους. Άρα μπορούμε να ταυτίσουμε ένα τέτοιο σύνολο με τα άκρα τους.
καθώς και οι ενώσεις τους η οι τομές τους τέμνονται αν και μόνο αν τέμνονται σε κάποιο άκρο τους. Άρα μπορούμε να ταυτίσουμε ένα τέτοιο σύνολο με τα άκρα τους.Χρησιμοποιώντας την αρχή εγκλεισμού- αποκλεισμού έχουμε
 .
.Αν
 τότε
τότε  .
.Επίσης έχουμε αν
 τότε
τότε  επειδή κάθε ζεύγος συνόλων τέμνονται από υπόθεση.
επειδή κάθε ζεύγος συνόλων τέμνονται από υπόθεση.Επίσης από υπόθεση, αν
 τότε
τότε  .
.Επίσης το πλήθος των υποσυνόλων του
 που περιέχουν δύο στοιχεία είναι
που περιέχουν δύο στοιχεία είναι  =
=  .
.Άρα
 .
.Νομίζω από αυτό μπορούμε να πάρουμε άτοπο. Δεν είμαι σίγουρος. Ας την συνεχίσει κάποιος άλλος.
Κωνσταντίνος Σμπώκος
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Ενδιαφέρουσα διάλεξη
Έστω,  ή πρώτη στιγμή που ο επιστήμονας
ή πρώτη στιγμή που ο επιστήμονας  κοιμόταν ταυτόχρονα με τον επιστήμονα
κοιμόταν ταυτόχρονα με τον επιστήμονα  , με
, με  και
και  .
.
Είναι προφανές ότι υπάρχουν ακριβώς τέτοιες στιγμές.
ακριβώς τέτοιες στιγμές.
Επίσης, θεωρούμε με
με  τις χρονικές στιγμές όπου ένας επιστήμονας αρχίζει να κοιμάται (
τις χρονικές στιγμές όπου ένας επιστήμονας αρχίζει να κοιμάται ( τέτοιες στιγμές για κάθε έναν από τους
τέτοιες στιγμές για κάθε έναν από τους  ).
).
Αν για κάποια ισχύει
ισχύει  τότε το ζητούμενο είναι προφανές (ακόμα και αν
τότε το ζητούμενο είναι προφανές (ακόμα και αν  ή
ή  ). Ας υποθέσουμε λοιπόν ότι όλα τα
). Ας υποθέσουμε λοιπόν ότι όλα τα  είναι διαφορετικά μεταξύ τους.
είναι διαφορετικά μεταξύ τους.
Τότε, σε κάθε μια από αυτές τις στιγμές, αντιστοιχεί μία από τις στιγμές . Πράγματι, αν η χρονική στιγμή
. Πράγματι, αν η χρονική στιγμή  δεν είναι μια από τις
δεν είναι μια από τις  , τότε θα μπορούσαμε να θεωρήσουμε μια άλλη στιγμή
, τότε θα μπορούσαμε να θεωρήσουμε μια άλλη στιγμή  όπου οι επιστήμονες
όπου οι επιστήμονες  κοιμούνται ταυτόχρονα. Αυτό όμως αντιβαίνει στον ορισμό των
κοιμούνται ταυτόχρονα. Αυτό όμως αντιβαίνει στον ορισμό των  .
.
Άρα, και αφού τα είναι διαφορετικά μεταξύ τους και αφού το πλήθος των
είναι διαφορετικά μεταξύ τους και αφού το πλήθος των  είναι ίσο με το πλήθος των
είναι ίσο με το πλήθος των  , σε κάθε ένα από τα
, σε κάθε ένα από τα  πρέπει να αντιστοιχεί ακριβώς ένα από τα
πρέπει να αντιστοιχεί ακριβώς ένα από τα  .
.
Ας θεωρήσουμε τώρα τους δύο επιστήμονες ώστε το
ώστε το 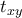 να είναι ελάχιστο. Από προηγούμενα, την στιγμή
να είναι ελάχιστο. Από προηγούμενα, την στιγμή 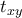 ακριβώς ένας από τους
ακριβώς ένας από τους  άρχισε να κοιμάται. Έστω ο
άρχισε να κοιμάται. Έστω ο  .
.
Ο τότε, προφανώς δεν μπορεί να άρχισε να κοιμάται την ίδια στιγμή με τον
τότε, προφανώς δεν μπορεί να άρχισε να κοιμάται την ίδια στιγμή με τον  . Άρα, όταν άρχισε να κοιμάται ο
. Άρα, όταν άρχισε να κοιμάται ο  , κανείς άλλος δεν κοιμόταν ήδη (αφού το
, κανείς άλλος δεν κοιμόταν ήδη (αφού το 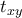 είναι ελάχιστο). Αυτό όμως αντιβαίνει στο γεγονός ότι σε κάθε
είναι ελάχιστο). Αυτό όμως αντιβαίνει στο γεγονός ότι σε κάθε  (στα οποία περιλαμβάνεται η στιγμή που άρχισε να κοιμάται ο
(στα οποία περιλαμβάνεται η στιγμή που άρχισε να κοιμάται ο  ), αντιστοιχεί ένα
), αντιστοιχεί ένα  .
.
Η απόδειξη ολοκληρώθηκε.
 ή πρώτη στιγμή που ο επιστήμονας
ή πρώτη στιγμή που ο επιστήμονας  κοιμόταν ταυτόχρονα με τον επιστήμονα
κοιμόταν ταυτόχρονα με τον επιστήμονα  , με
, με  και
και  .
.Είναι προφανές ότι υπάρχουν
 ακριβώς τέτοιες στιγμές.
ακριβώς τέτοιες στιγμές.Επίσης, θεωρούμε
 με
με  τις χρονικές στιγμές όπου ένας επιστήμονας αρχίζει να κοιμάται (
τις χρονικές στιγμές όπου ένας επιστήμονας αρχίζει να κοιμάται ( τέτοιες στιγμές για κάθε έναν από τους
τέτοιες στιγμές για κάθε έναν από τους  ).
).Αν για κάποια
 ισχύει
ισχύει  τότε το ζητούμενο είναι προφανές (ακόμα και αν
τότε το ζητούμενο είναι προφανές (ακόμα και αν  ή
ή  ). Ας υποθέσουμε λοιπόν ότι όλα τα
). Ας υποθέσουμε λοιπόν ότι όλα τα  είναι διαφορετικά μεταξύ τους.
είναι διαφορετικά μεταξύ τους.Τότε, σε κάθε μια από αυτές τις στιγμές, αντιστοιχεί μία από τις στιγμές
 . Πράγματι, αν η χρονική στιγμή
. Πράγματι, αν η χρονική στιγμή  δεν είναι μια από τις
δεν είναι μια από τις  , τότε θα μπορούσαμε να θεωρήσουμε μια άλλη στιγμή
, τότε θα μπορούσαμε να θεωρήσουμε μια άλλη στιγμή  όπου οι επιστήμονες
όπου οι επιστήμονες  κοιμούνται ταυτόχρονα. Αυτό όμως αντιβαίνει στον ορισμό των
κοιμούνται ταυτόχρονα. Αυτό όμως αντιβαίνει στον ορισμό των  .
.Άρα, και αφού τα
 είναι διαφορετικά μεταξύ τους και αφού το πλήθος των
είναι διαφορετικά μεταξύ τους και αφού το πλήθος των  είναι ίσο με το πλήθος των
είναι ίσο με το πλήθος των  , σε κάθε ένα από τα
, σε κάθε ένα από τα  πρέπει να αντιστοιχεί ακριβώς ένα από τα
πρέπει να αντιστοιχεί ακριβώς ένα από τα  .
.Ας θεωρήσουμε τώρα τους δύο επιστήμονες
 ώστε το
ώστε το 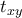 να είναι ελάχιστο. Από προηγούμενα, την στιγμή
να είναι ελάχιστο. Από προηγούμενα, την στιγμή 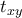 ακριβώς ένας από τους
ακριβώς ένας από τους  άρχισε να κοιμάται. Έστω ο
άρχισε να κοιμάται. Έστω ο  .
. Ο
 τότε, προφανώς δεν μπορεί να άρχισε να κοιμάται την ίδια στιγμή με τον
τότε, προφανώς δεν μπορεί να άρχισε να κοιμάται την ίδια στιγμή με τον  . Άρα, όταν άρχισε να κοιμάται ο
. Άρα, όταν άρχισε να κοιμάται ο  , κανείς άλλος δεν κοιμόταν ήδη (αφού το
, κανείς άλλος δεν κοιμόταν ήδη (αφού το 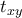 είναι ελάχιστο). Αυτό όμως αντιβαίνει στο γεγονός ότι σε κάθε
είναι ελάχιστο). Αυτό όμως αντιβαίνει στο γεγονός ότι σε κάθε  (στα οποία περιλαμβάνεται η στιγμή που άρχισε να κοιμάται ο
(στα οποία περιλαμβάνεται η στιγμή που άρχισε να κοιμάται ο  ), αντιστοιχεί ένα
), αντιστοιχεί ένα  .
.Η απόδειξη ολοκληρώθηκε.
Κερδίζουμε ό,τι τολμούμε!
Re: Ενδιαφέρουσα διάλεξη
Δείτε και εδώ https://artofproblemsolving.com/communi ... 68p2403861
Πίσω από το πρόβλημα κρύβεται το Θεώρημα Helly.
Πίσω από το πρόβλημα κρύβεται το Θεώρημα Helly.
Σιλουανός Μπραζιτίκος
Re: Ενδιαφέρουσα διάλεξη
Να ολοκληρώσω την απόδειξη. Έστωstranger έγραψε: ↑Τρί Σεπ 01, 2020 9:59 pmTo ποστ μου νούμερο 2 είναι λανθασμένο. Ευχαριστώ το Σταύρο για την επισήμανση.
Ας κάνω άλλη μια προσπάθεια.Έστω ότι δεν υπάρχει στιγμή που να κοιμήθηκαν τρεις επιστήμονες μαζί.
Παρατηρούμε ότι τα σύνολακαθώς και οι ενώσεις τους η οι τομές τους τέμνονται αν και μόνο αν τέμνονται σε κάποιο άκρο τους. Άρα μπορούμε να ταυτίσουμε ένα τέτοιο σύνολο με τα άκρα τους.
Χρησιμοποιώντας την αρχή εγκλεισμού- αποκλεισμού έχουμε
.
Αντότε
.
Επίσης έχουμε αντότε
επειδή κάθε ζεύγος συνόλων τέμνονται από υπόθεση.
Επίσης από υπόθεση, αντότε
.
Επίσης το πλήθος των υποσυνόλων τουπου περιέχουν δύο στοιχεία είναι
=
.
Άρα.
Νομίζω από αυτό μπορούμε να πάρουμε άτοπο. Δεν είμαι σίγουρος. Ας την συνεχίσει κάποιος άλλος.
 το ελάχιστο σημείο τομής των
το ελάχιστο σημείο τομής των  και
και  .
.Τότε επειδή δεν υπάρχει σημείο τομής τριών συνόλων έχουμε ότι το πλήθος των
 είναι
είναι 
 .
.Άρα σύμφωνα με τα παραπάνω που έγραψα έχουμε
 , το οποίο σημαίνει ότι υπάρχουν ακριβώς 10 διακεκριμμένα άκρα
, το οποίο σημαίνει ότι υπάρχουν ακριβώς 10 διακεκριμμένα άκρα  .
.Άρα έχουμε ότι το
 είναι το ελάχιστο σημείο τομής ενός
είναι το ελάχιστο σημείο τομής ενός  και
και  , όπου
, όπου ![A_i = [x_i,y_i] \cup [k_i,a_{10}] A_i = [x_i,y_i] \cup [k_i,a_{10}]](/forum/ext/geomar/texintegr/latexrender/pictures/f271acece84f9852a3f0d1bfe8acf971.png) και
και ![A_j = [x_j,y_j] \cup [k_j,a_{10}] A_j = [x_j,y_j] \cup [k_j,a_{10}]](/forum/ext/geomar/texintegr/latexrender/pictures/843651983224b760e6a0f7a9d84da2bd.png) . Όμως τα δύο αυτά σύνολα τέμνονται στο
. Όμως τα δύο αυτά σύνολα τέμνονται στο  το οποίο είναι άτοπο και το συμπέρασμα έπεται.
το οποίο είναι άτοπο και το συμπέρασμα έπεται.Κωνσταντίνος Σμπώκος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες
