Μερικές εξισώσεις για τον Θαλή
Δημοσιεύτηκε: Τρί Νοέμ 07, 2017 10:12 pm
Μερικές εξισώσεις για τον "Θαλή".
1.

2.
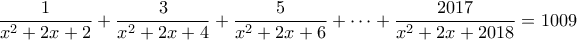
3.

4.

1.

2.
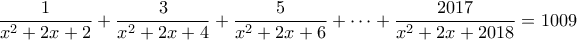
3.

4.

https://www.mathematica.gr/forum/
https://www.mathematica.gr/forum/viewtopic.php?f=177&t=60190

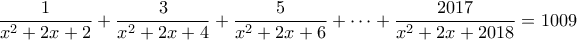


Κάνουμε ρητούς τους πανομαστές και έχουμε:
 ή
ή 
 ή
ή  έχουμε :
έχουμε : 



 ή
ή 
Έστω
 ,
,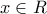 , τότε
, τότε![f'(x)=5[(x-1)^4+(x-2)^4+\cdots +(x-2017)^4]>0 f'(x)=5[(x-1)^4+(x-2)^4+\cdots +(x-2017)^4]>0](/forum/ext/geomar/texintegr/latexrender/pictures/b361ed202363a726c1ca08a0468e70fe.png) άρα η
άρα η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.![f(x)=(x-1)^5+(x-2)^5+ \cdots +(x-2017)^5=[(x-1)^5+(x-2017)^5]+ [(x-2)^5 + (x-2016)^5] f(x)=(x-1)^5+(x-2)^5+ \cdots +(x-2017)^5=[(x-1)^5+(x-2017)^5]+ [(x-2)^5 + (x-2016)^5]](/forum/ext/geomar/texintegr/latexrender/pictures/8a663b5cde65ffa944dd623a1581f02e.png)

![=2(x-1009)[(x-1)^4 - (x-1)^3(x-2017) +(x-1)^2(x-2017)^2 -(x-1)(x-2017)^3 +(x-2017)^4] + =2(x-1009)[(x-1)^4 - (x-1)^3(x-2017) +(x-1)^2(x-2017)^2 -(x-1)(x-2017)^3 +(x-2017)^4] +](/forum/ext/geomar/texintegr/latexrender/pictures/614a73077f800f1ee380ff83dfdc60ef.png)

![+(x-2016)^4] + \cdots + (x-1009)^5 +(x-2016)^4] + \cdots + (x-1009)^5](/forum/ext/geomar/texintegr/latexrender/pictures/ccb578a590b83b9617a5fd279d53a2a4.png)
 έχει ρίζα το
έχει ρίζα το  που είναι και η μοναδική λόγω μονοτονίας.
που είναι και η μοναδική λόγω μονοτονίας. , οπότε :
, οπότε : 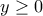 και :
και : 

 .
.To πλήθος των κλασμάτων είναι
 και καθένα από αυτά είναι μικρότερο ή ίσο της μονάδας, αφού με
και καθένα από αυτά είναι μικρότερο ή ίσο της μονάδας, αφού με  είναι:
είναι: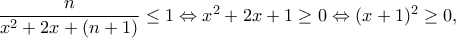

 .
.Θέτουμε όπου
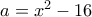 και όπου
και όπου  .
.
 με ισότητα μόνο όταν
με ισότητα μόνο όταν  .
. , δηλαδή
, δηλαδή  , που είναι δεκτή.
, που είναι δεκτή.
Μάλλον αυτή η εβδομάδα στο mathematica ειναι αφιερωμένη στην Βαβυλώνα!!!
 , ο θεματοδότης παραπέμπει στο τέχνασμα Θάνου .
, ο θεματοδότης παραπέμπει στο τέχνασμα Θάνου .Δεν καταλαβαίνω τον σκοπό της ανάρτησης.Τσιαλας Νικολαος έγραψε: ↑Πέμ Νοέμ 01, 2018 2:58 pmΕπαναφέρω μετά από πολύ καιρό... Μπορεί η άσκηση 6 να λυθεί με άλλους τρόπους χωρίς αυτό το υπέροχο τεχνασμα?
Υ.γ: η πρώτη λύση μου ήρθε κατά την διάρκεια του ύπνου μου! Η δεύτερη την ώρα που έδειχνα την πρώτη στους μαθητές!
Απλά να δουμε αν υπάρχουν και άλλοι τρόποι... σίγουρα εγώ εχω 2 ακόμη! Μάλιστα σε μια ανάλογη εξίσωση ο Andreescu χρησιμοποιεί την έκφραση "αν είμαστε τυχεροί " βρίσκουμε.... Σκέφτηκα λοιπόν μήπως μπορούμε να βρούμε και άλλους!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Νοέμ 01, 2018 5:04 pmΔεν καταλαβαίνω τον σκοπό της ανάρτησης.Τσιαλας Νικολαος έγραψε: ↑Πέμ Νοέμ 01, 2018 2:58 pmΕπαναφέρω μετά από πολύ καιρό... Μπορεί η άσκηση 6 να λυθεί με άλλους τρόπους χωρίς αυτό το υπέροχο τεχνασμα?
Υ.γ: η πρώτη λύση μου ήρθε κατά την διάρκεια του ύπνου μου! Η δεύτερη την ώρα που έδειχνα την πρώτη στους μαθητές!
Η ερώτηση είναι αν υπάρχουν και άλλες λύσεις;
η ότι γνωρίζεις άλλες δύο λύσεις και θέλεις να γραφούν;
Πάντως στην δεύτερη περίπτωση θα μπορούσες να γράψεις τουλάχιστον την μία.
Καλησπέρα.Τσιαλας Νικολαος έγραψε: ↑Πέμ Νοέμ 01, 2018 2:58 pmΕπαναφέρω μετά από πολύ καιρό... Μπορεί η άσκηση 6 να λυθεί με άλλους τρόπους χωρίς αυτό το υπέροχο τεχνασμα?



