Είναι ένα θέμα εμπνευσμένο από μια άσκηση του βιβλίου "Μαθηματικοί Διαγωνισμοί 1" Χαράλαμπου Στεργίου και Σιλουανού Μπραζιτίκου.
Έχω βρεί μια λύση εγώ αλλα θα ήθελα και άλλες ιδέες.
Έστω
 θετικοί πραγματικοί αριθμοί. Να αποδείχθεί πως:
θετικοί πραγματικοί αριθμοί. Να αποδείχθεί πως: 
Πότε ισχύει η ισότητα;
(Ζητώ συγνώμη για αυτή την άβολη χρήση LaTex.)

 Οπότε έχουμε να αποδείξουμε ότι
Οπότε έχουμε να αποδείξουμε ότι
 ,
,
 και
και 





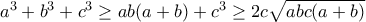
 και
και 

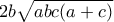 και
και 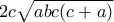

 , οπότε αρκεί
, οπότε αρκεί  .
. , οπότε αρκεί
, οπότε αρκεί  , που είναι η ΑM-GM.
, που είναι η ΑM-GM.



 , με ισότητα και στα τρία μέλη αν και μόνο αν
, με ισότητα και στα τρία μέλη αν και μόνο αν  .
.

 . Ισότητα όταν
. Ισότητα όταν 

 , ισότητα όταν
, ισότητα όταν 
 .
.