 ικνανοποιείται η ισότητα
ικνανοποιείται η ισότητα ;
;Για Θαλή/Ευκλείδη Γ' Λυκείου. Πηγή το ρωσικό περιοδικό "Τα μαθηματικά στο σχολείο"
Συντονιστές: achilleas, emouroukos, silouan
 ικνανοποιείται η ισότητα
ικνανοποιείται η ισότητα ;
;ΘέτουμεAl.Koutsouridis έγραψε: ↑Δευ Σεπ 16, 2019 11:41 pmΓια ποιές μη αρνητικές τιμές τωνικνανοποιείται η ισότητα
;
Για Θαλή/Ευκλείδη Γ' Λυκείου

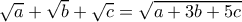 (1)
(1)
 τότε έχουμε την προφανή λύση όλα
τότε έχουμε την προφανή λύση όλα 






 είναι
είναι  η
η 



 είναι
είναι 
 ώστε να ισχύει η ισότητα.
ώστε να ισχύει η ισότητα. και
και  .
. και
και  . Έχουμε λοιπόν
. Έχουμε λοιπόν  οπότε η ισότητα λαμβάνεται αν και μόνο αν τα
οπότε η ισότητα λαμβάνεται αν και μόνο αν τα 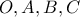 είναι συνευθειακά και με αυτήν την σειρά.
είναι συνευθειακά και με αυτήν την σειρά. , επειδή
, επειδή  πρέπει
πρέπει 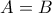 και άρα και
και άρα και  . Αντιστρόφως αν
. Αντιστρόφως αν  τότε ισχύει η ισότητα.
τότε ισχύει η ισότητα.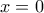 αλλά
αλλά  , επειδή
, επειδή  πρέπει
πρέπει  και άρα και
και άρα και  . Αντιστρόφως αν
. Αντιστρόφως αν  τότε ισχύει η ισότητα.
τότε ισχύει η ισότητα.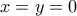 τότε ισχύει η ισότητα.
τότε ισχύει η ισότητα. είναι ίσα με
είναι ίσα με  .
.
 τους όρους του αθροίσματους του αριστερού μέλους της. Παρατηρούμε ότι
τους όρους του αθροίσματους του αριστερού μέλους της. Παρατηρούμε ότι  και η εξίσωση μπορεί να γραφεί στην μορφή
και η εξίσωση μπορεί να γραφεί στην μορφή


 , έχουμε όμως
, έχουμε όμως  και
και 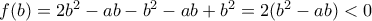 . Άρα δεν υπάρχουν θετικές λύσεις στο εν λόγω διάστημα. Οι όποιες λύσεις θα πρέπει να έχουν τουλάχιστον μια μεταβλητή ίση με το μηδέν και συνεχίζουμε εύκολα από αυτό το σημείο...
. Άρα δεν υπάρχουν θετικές λύσεις στο εν λόγω διάστημα. Οι όποιες λύσεις θα πρέπει να έχουν τουλάχιστον μια μεταβλητή ίση με το μηδέν και συνεχίζουμε εύκολα από αυτό το σημείο...Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες