
γνωρίζουμε ότι έχει πραγματικές ρίζες.
Αν ισχύει

να δειχθεί ότι ακριβώς μία ρίζα της βρίσκεται στο διάστημα

Συντονιστές: achilleas, emouroukos, silouan



ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Οκτ 07, 2020 9:03 pmΗ εξίσωση
γνωρίζουμε ότι έχει πραγματικές ρίζες.
Αν ισχύει
να δειχθεί ότι ακριβώς μία ρίζα της βρίσκεται στο διάστημα
 . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι  , Καθώς από το θεώρημα Bolzano προκύπτει ότι θα υπάρχει ρίζα στο διάστημα
, Καθώς από το θεώρημα Bolzano προκύπτει ότι θα υπάρχει ρίζα στο διάστημα  και από την μορφή της παραγώγου της
και από την μορφή της παραγώγου της  ,
,  η συνάρτηση σε αυτό το διάστημα είναι είτε γνησίως αύξουσα, είτε γνησίως φθίνουσα. Άρα η ρίζα θα είναι μοναδική. Δηλαδή αρκεί να δείξουμε ότι ισχύει
η συνάρτηση σε αυτό το διάστημα είναι είτε γνησίως αύξουσα, είτε γνησίως φθίνουσα. Άρα η ρίζα θα είναι μοναδική. Δηλαδή αρκεί να δείξουμε ότι ισχύει  . Η τελευταία ανίσωση ισοδύναμα γράφεται:
. Η τελευταία ανίσωση ισοδύναμα γράφεται: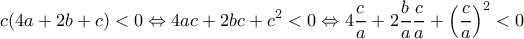 . (1)
. (1) και
και  , τότε η συνθήκη για τα
, τότε η συνθήκη για τα  γράφεται
γράφεται

 προκύπτουν οι ανισώσεις
προκύπτουν οι ανισώσεις

 (2)
(2) .
. και εφόσον
και εφόσον  , η παραπάνω ανίσωση μπορεί να γραφεί
, η παραπάνω ανίσωση μπορεί να γραφεί
 , τότε
, τότε  (3)
(3) που ικανοποιούν την (3) στο καρτεσιανό επίπεδο είναι τα εσωτερικά σημεία του κύκλου με κέντρο το σημείο
που ικανοποιούν την (3) στο καρτεσιανό επίπεδο είναι τα εσωτερικά σημεία του κύκλου με κέντρο το σημείο  και ακτίνα
και ακτίνα  . Λόγω της (2) από αυτά τα σημεία θεωρούμε μόνο αυτά για το οποία
. Λόγω της (2) από αυτά τα σημεία θεωρούμε μόνο αυτά για το οποία  . (το σκούρο τμήμα του κυκλικού δίσκου στο παρακάτω σχήμα).
. (το σκούρο τμήμα του κυκλικού δίσκου στο παρακάτω σχήμα). προκύπτει άλλο ένα τμήμα κυκλικού δίσκου, συμμετρικό του παραπάνω ως προς την ευθεία
προκύπτει άλλο ένα τμήμα κυκλικού δίσκου, συμμετρικό του παραπάνω ως προς την ευθεία  . Όμως
. Όμως 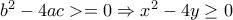 . Οπότε στην περίπτωσή μας θεωρούμε μόνο το κομμάτι του δίσκου που προκύπτει από τις (2) και (3).
. Οπότε στην περίπτωσή μας θεωρούμε μόνο το κομμάτι του δίσκου που προκύπτει από τις (2) και (3). , έχουμε (
, έχουμε (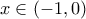 ).
).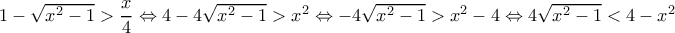
 και ανίσωση γίνεται
και ανίσωση γίνεται

 , η ανίσωση ισχύει για
, η ανίσωση ισχύει για  .
.
 . Επομένως αρκεί να δείξουμε ότι
. Επομένως αρκεί να δείξουμε ότι  . Το οποίο εύκολα βλέπουμε ότι ισχύει, αφού
. Το οποίο εύκολα βλέπουμε ότι ισχύει, αφού  (θετικό) και
(θετικό) και  ( από το σχήμα).
( από το σχήμα).  και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.Καλημέρα Αλέξανδρε.Al.Koutsouridis έγραψε: ↑Σάβ Οκτ 10, 2020 2:16 amΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Οκτ 07, 2020 9:03 pmΗ εξίσωση
γνωρίζουμε ότι έχει πραγματικές ρίζες.
Αν ισχύει
να δειχθεί ότι ακριβώς μία ρίζα της βρίσκεται στο διάστημα
. Αρκεί να δείξουμε ότι
, Καθώς από το θεώρημα Bolzano προκύπτει ότι θα υπάρχει ρίζα στο διάστημα
και από την μορφή της παραγώγου της
,
η συνάρτηση σε αυτό το διάστημα είναι είτε γνησίως αύξουσα, είτε γνησίως φθίνουσα. Άρα η ρίζα θα είναι μοναδική. Δηλαδή αρκεί να δείξουμε ότι ισχύει
.
 και
και  τότε η
τότε η  έχει άνισες πραγματικές ρίζες και
έχει άνισες πραγματικές ρίζες και  .
.Καλημέρα κ.Σταύρο,ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Οκτ 11, 2020 9:09 am
Καλημέρα Αλέξανδρε.
Αυτό που κράτησα από την λύση σου προκύπτει καθαρά με θεωρία τριωνύμου.
Δηλαδή ανκαι
τότε η
έχει άνισες πραγματικές ρίζες και
ακριβώς μία βρίσκεται μεταξύ των.
Η λύση λοιπόν δεν χρησιμοποιεί την υπόθεση ότι η εξίσωση έχει άνισες πραγματικές ρίζες.
Η απόδειξη μου είναι διαφορετική και το χρησιμοποιεί.
Είναι με ύλη Α Λυκείου.
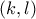 το διάστημά μας και
το διάστημά μας και  οι δυο άνισες ρίζες του τριώνυμου. Τότε η συνθήκη θα μεταφράζεται είτε σε
οι δυο άνισες ρίζες του τριώνυμου. Τότε η συνθήκη θα μεταφράζεται είτε σε  είτε
είτε  .
. από τις προτάσεις
από τις προτάσεις  στις παραπάνω παραπομπές έχουμε
στις παραπάνω παραπομπές έχουμε και
και  οπότε
οπότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες