Χριστουγεννιάτικη εξίσωση
Συντονιστές: achilleas, emouroukos, silouan
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Χριστουγεννιάτικη εξίσωση
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 3:14 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
-
giannispapav
- Δημοσιεύσεις: 70
- Εγγραφή: Πέμ Σεπ 14, 2017 5:59 pm
Re: Χριστουγεννιάτικη εξίσωση
Το αριστερό μέλος έχει ολικό ελάχιστο το  για
για  ενώ το δεξί μέλος έχει ολικό μέγιστο για
ενώ το δεξί μέλος έχει ολικό μέγιστο για  το
το  . Επομένως μοναδική λύση της εξίσωσης είναι το
. Επομένως μοναδική λύση της εξίσωσης είναι το  .
.
 για
για  ενώ το δεξί μέλος έχει ολικό μέγιστο για
ενώ το δεξί μέλος έχει ολικό μέγιστο για  το
το  . Επομένως μοναδική λύση της εξίσωσης είναι το
. Επομένως μοναδική λύση της εξίσωσης είναι το  .
.-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Χριστουγεννιάτικη εξίσωση
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 3:14 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
giannispapav
- Δημοσιεύσεις: 70
- Εγγραφή: Πέμ Σεπ 14, 2017 5:59 pm
Re: Χριστουγεννιάτικη εξίσωση
Έχουμε 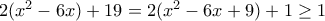 άρα
άρα 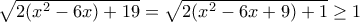 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.
Επίσης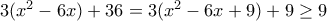 άρα
άρα 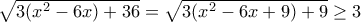 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.
Άρα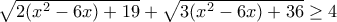 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.
Τέλος έχουμε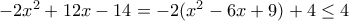 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.
Έτσι,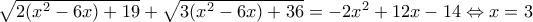 .
.
Το η ΚΥΜΕ είχε βάλει ως θέμα 4 της Β λυκείου να λυθεί η εξίσωση
η ΚΥΜΕ είχε βάλει ως θέμα 4 της Β λυκείου να λυθεί η εξίσωση 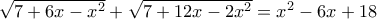 .
.
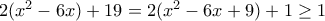 άρα
άρα 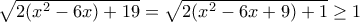 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.Επίσης
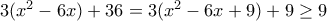 άρα
άρα 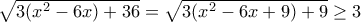 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.Άρα
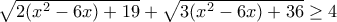 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
.Τέλος έχουμε
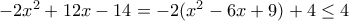 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  .
. Έτσι,
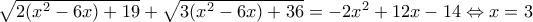 .
.Το
 η ΚΥΜΕ είχε βάλει ως θέμα 4 της Β λυκείου να λυθεί η εξίσωση
η ΚΥΜΕ είχε βάλει ως θέμα 4 της Β λυκείου να λυθεί η εξίσωση 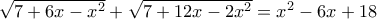 .
.-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Χριστουγεννιάτικη εξίσωση
Η απόδειξη είναι απλή:orestisgotsis έγραψε: ↑Τρί Δεκ 26, 2023 2:26 pmΑυτά όμως που γράφετε δεν έχουν απόδειξη;giannispapav έγραψε: ↑Τρί Δεκ 26, 2023 2:18 pmΤο αριστερό μέλος έχει ολικό ελάχιστο τογια
ενώ το δεξί μέλος έχει ολικό μέγιστο για
το
. Επομένως μοναδική λύση της εξίσωσης είναι το
.
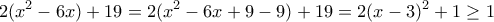
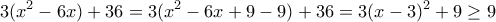
Άρα το πρώτο μέλος είναι μεγαλύτερο ή ίσο από το
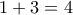 . Και αφού για
. Και αφού για  ισχύει η ισότητα, άρα η ελάχιστη τιμή
ισχύει η ισότητα, άρα η ελάχιστη τιμήπου μπορεί να πάρει το πρώτο μέλος είναι το
 , όταν
, όταν 
Όμοια
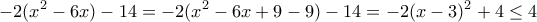
Άρα το δεύτερο μέλος έχει μέγιστη τιμή το
 , όταν
, όταν  .
. Συνεπώς η δοσμένη εξίσωση έχει την λύση

- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Χριστουγεννιάτικη εξίσωση
Η εξίσωση γράφεται:
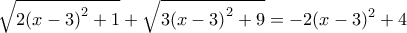
Θέτω
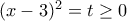 και έχω
και έχω 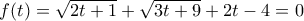
H εξίσωση έχει την προφανή λύση
 κι επειδή
κι επειδή 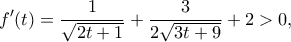
η συνάρτηση
 είναι γνησίως αύξουσα, οπότε
είναι γνησίως αύξουσα, οπότε  είναι η μοναδική ρίζα της εξίσωσης, άρα
είναι η μοναδική ρίζα της εξίσωσης, άρα 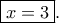
τελευταία επεξεργασία από george visvikis σε Τετ Δεκ 27, 2023 4:46 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Χριστουγεννιάτικη εξίσωση
Πιο απλά ακόμα (στην ουσία το ίδιο είναι) : 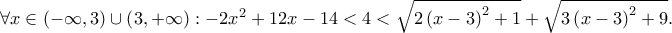
Η απόδειξη για την δεξιά βγάζει μάτι. Για την αριστερή,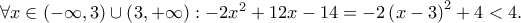
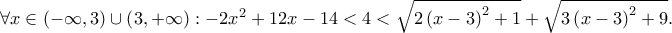
Η απόδειξη για την δεξιά βγάζει μάτι. Για την αριστερή,
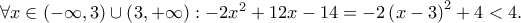
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες

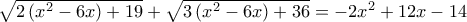 .
.