 της προέκτασης της διαμέτρου
της προέκτασης της διαμέτρου  ενός ημικυκλίου , φέρω το εφαπτόμενο
ενός ημικυκλίου , φέρω το εφαπτόμενοτμήμα
 . Η διχοτόμος της γωνίας
. Η διχοτόμος της γωνίας  , τέμνει την
, τέμνει την  στο σημείο
στο σημείο  και το τόξο στο
και το τόξο στο  .
.α) Δείξτε ότι :
 ... β) Βρείτε τη θέση του
... β) Βρείτε τη θέση του  για την οποία τα τμήματα
για την οποία τα τμήματα 
είναι παράλληλα ( επιτρέπεται και μη κατασκευαστική - δηλαδή υπολογιστική - λύση ) .






 και
και 
 κι επειδή
κι επειδή 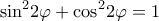
 , όπου το
, όπου το ![\boxed{x = \frac{R}{3}\left( { - 2 + \sqrt[3]{{73 - 6\sqrt {87} }} + \sqrt[3]{{73 + 6\sqrt {87} }}} \right)} \boxed{x = \frac{R}{3}\left( { - 2 + \sqrt[3]{{73 - 6\sqrt {87} }} + \sqrt[3]{{73 + 6\sqrt {87} }}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/ab2a65b4d4b25f57f9ce14863b4035d5.png)
 θα είναι :
θα είναι : 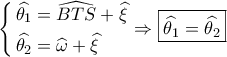 και αφού
και αφού  . Για το άλλο ερώτημα .
. Για το άλλο ερώτημα . είναι όμοια. Αν
είναι όμοια. Αν 
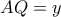 θα ισχύουν :
θα ισχύουν :  απ’ όπου
απ’ όπου ![\boxed{y = \frac{R}{3}(\sqrt[3]{{28 - 3\sqrt {87} }} + \sqrt[3]{{28 + 3\sqrt {87} }}) - \frac{{2R}}{3}} \boxed{y = \frac{R}{3}(\sqrt[3]{{28 - 3\sqrt {87} }} + \sqrt[3]{{28 + 3\sqrt {87} }}) - \frac{{2R}}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/e2fa03bbd20bf35197fa38145453b0d2.png) . Φέρνω το
. Φέρνω το  ή
ή  τέμνει την
τέμνει την  στο
στο