Ανάλυση
Βήμα πρώτο
- Μεγάλες κατακευές_4_ανάλυση_1.png (8.86 KiB) Προβλήθηκε 494 φορές
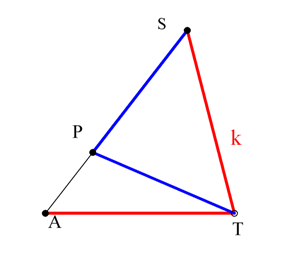
Θεωρώ πρώτα- πρώτα ισοσκελές τρίγωνο

και σημείο

της

για το οποίο

και

.
Από την τελευταία προκύπτουν άμεσα ότι :

και η ευθεία

εφάπτεται του κύκλου που διέρχεται από τα

.
Έτσι

Βήμα δεύτερο .

- Μεγάλες κατακευές_4_ανάλυση_2.png (18.31 KiB) Προβλήθηκε 494 φορές
Φέρνω από το

παράλληλη στην

που τέμνει τα ύψη του ισοσκελούς τριγώνου

, τα

στα

αντίστοιχα . Προφανώς :
Το

είναι μέσο του

,άρα το

είναι το βαρύκεντρο του τριγώνου

.
Αν η ευθεία
τμήση την

στο

αυτό θα είναι μέσο του

.
Επειδή τα

βλέπουν υπό ορθή γωνία την

από το εγγράψιμο τετράπλευρο

και λόγω της

έχω :

και άρα

Βήμα. Τρίτο.

- Μεγάλες κατακευές_4_ανάλυση_3.png (29.21 KiB) Προβλήθηκε 494 φορές
Φέρνω τώρα και τη διατέμνουσα

στο ορθογώνιο τρίγωνο

και από το Θ. Μενελάου έχω :

Η τελευταία μας εξασφαλίζει:

.
Συνεπώς το τρίγωνο

είναι ισοσκελές , το τραπέζιο

είναι ισοσκελές.
Έστω λοιπόν

το κέντρο του περιγεγραμμένου κύκλου στο τραπέζιο αυτό και

η διάμετρος από το

. Προφανώς η ευθεία

και άρα η ευθεία
διέρχεται στο μέσο

της ακτίνας
. Επειδή δε η
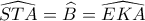
( υπό χορδής κι εφαπτομένης) τα ορθογώνια τρίγωνα ,

είναι όμοια.
Αφού τώρα

.
Κατασκευή :

- μεγάλες καρασκευές 4_Κατασκευή.png (19.17 KiB) Προβλήθηκε 486 φορές
Με κέντρο το μέσο

της ακτίνας
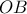
γράφω τον κύκλο

. Η εφαπτομένη
του κύκλου αυτού( μέσα στο

) από το

τέμνει τον κύκλο

στο

.
Φέρνω την εφαπτομένη του κύκλου

στο

που τέμνει τον κύκλο

στο

. Η

τέμνει τον κύκλο

στο ζητούμενο σημείο

( Τα

εκατέρωθεν της

)
 και μας ζητήθηκε να εντοπίσουμε
και μας ζητήθηκε να εντοπίσουμε , ώστε προεκτείνοντας την
, ώστε προεκτείνοντας την  κατά τμήμα
κατά τμήμα 
 , να προκύψει :
, να προκύψει :  .
. , με
, με  , υψώνω κάθετη
, υψώνω κάθετη 
 το μέσο της
το μέσο της 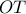 . Η
. Η  τέμνει το τόξο στο
τέμνει το τόξο στο 

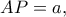 τότε έχουμε
τότε έχουμε  και
και 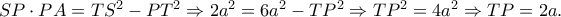
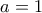 κατασκευάζουμε κάπου ένα τρίγωνο
κατασκευάζουμε κάπου ένα τρίγωνο  , ώστε
, ώστε 
 και προσδιορίζουμε το
και προσδιορίζουμε το και γωνία
και γωνία και προσδιορίζουμε το
και προσδιορίζουμε το

 και
και 
 , συναρτήσει της ακτίνας
, συναρτήσει της ακτίνας  . Αυτό μπορεί να γίνει είτε
. Αυτό μπορεί να γίνει είτε  , κάτι πολύ κοπιαστικό ,
, κάτι πολύ κοπιαστικό , , δίνεται από τον τύπο :
, δίνεται από τον τύπο : , η οποία επιλυόμενη με τα δεδομένα
, η οποία επιλυόμενη με τα δεδομένα , μήκος εύκολα κατασκευάσιμο .
, μήκος εύκολα κατασκευάσιμο .  και σημείο
και σημείο  για το οποίο
για το οποίο  και
και  .
. και η ευθεία
και η ευθεία  .
.
 που τέμνει τα ύψη του ισοσκελούς τριγώνου
που τέμνει τα ύψη του ισοσκελούς τριγώνου  , τα
, τα  στα
στα  αντίστοιχα . Προφανώς :
αντίστοιχα . Προφανώς :  είναι μέσο του
είναι μέσο του  είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου 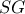 τμήση την
τμήση την  αυτό θα είναι μέσο του
αυτό θα είναι μέσο του  βλέπουν υπό ορθή γωνία την
βλέπουν υπό ορθή γωνία την  και λόγω της
και λόγω της  έχω :
έχω : 

 στο ορθογώνιο τρίγωνο
στο ορθογώνιο τρίγωνο  και από το Θ. Μενελάου έχω :
και από το Θ. Μενελάου έχω :  Η τελευταία μας εξασφαλίζει:
Η τελευταία μας εξασφαλίζει:  .
.  είναι ισοσκελές , το τραπέζιο
είναι ισοσκελές , το τραπέζιο  είναι ισοσκελές.
είναι ισοσκελές. το κέντρο του περιγεγραμμένου κύκλου στο τραπέζιο αυτό και
το κέντρο του περιγεγραμμένου κύκλου στο τραπέζιο αυτό και  η διάμετρος από το
η διάμετρος από το  . Προφανώς η ευθεία
. Προφανώς η ευθεία  και άρα η ευθεία
και άρα η ευθεία 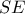 διέρχεται στο μέσο
διέρχεται στο μέσο  της ακτίνας
της ακτίνας 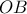 . Επειδή δε η
. Επειδή δε η 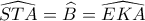
 είναι όμοια.
είναι όμοια. .
. . Η εφαπτομένη
. Η εφαπτομένη  ) από το
) από το  στο
στο 
 . Η
. Η  τέμνει τον κύκλο
τέμνει τον κύκλο  εκατέρωθεν της
εκατέρωθεν της