 , ακτίνας
, ακτίνας  .
.Η διαγώνιος
 διέρχεται από το σημείο
διέρχεται από το σημείο  , ενώ η γωνία
, ενώ η γωνία  είναι ορθή .
είναι ορθή .Υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου .
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , ακτίνας
, ακτίνας  .
. διέρχεται από το σημείο
διέρχεται από το σημείο  , ενώ η γωνία
, ενώ η γωνία  είναι ορθή .
είναι ορθή ..
 η γωνία των διαγωνίων
η γωνία των διαγωνίων  . Τότε,
. Τότε,  .
. χορδές του κύκλου
χορδές του κύκλου  , άρα
, άρα  .
.  και επιτυγχάνεται όταν
και επιτυγχάνεται όταν  και
και  .
. τ.μ.
τ.μ.Γεια σου Γιώργο.Γιώργος Ρίζος έγραψε: ↑Δευ Ιουν 18, 2018 5:37 pmΚαλησπέρα σε όλους.
Ισχύει η γνωστή πρόταση:
Από όλα τα εγγεγραμμένα ν-γωνα σε έναν κύκλο μέγιστο εμβαδόν έχει το κανονικό.
Οπότε το τετράγωνο με διαγώνιες πάνω στους άξονες πληροί τα δεδομένα του προβλήματος κι έχει μέγιστο εμβαδόν ίσο μετ.μ.
 εγγεγραμμένο σε κύκλο.
εγγεγραμμένο σε κύκλο. στο τόξο
στο τόξο  , ώστε
, ώστε  . Τότε
. Τότε  , με το ίσον να ισχύει όταν το
, με το ίσον να ισχύει όταν το  ταυτίζεται με το
ταυτίζεται με το  .
.  και
και  (1) θα είναι
(1) θα είναι  . Η απόδειξη της (1) είναι απλή.
. Η απόδειξη της (1) είναι απλή. .
.  σημείο στο τόξο
σημείο στο τόξο 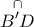 , ώστε
, ώστε  . Τότε
. Τότε  , με το ίσον να ισχύει όταν το
, με το ίσον να ισχύει όταν το  ταυτίζεται με το
ταυτίζεται με το  .
. 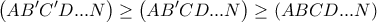 .
.  , οπότε το θέμα καθίσταται αρκετά δυσκολότερο ...
, οπότε το θέμα καθίσταται αρκετά δυσκολότερο ...Είχα διαισθανθεί ότι ζητούσες κάτι τέτοιο, (αλλιώς δεν είχε νόημα η
 να διέρχεται από το σημείο
να διέρχεται από το σημείο  ), γι αυτό και την έλυσα από χτες. Είναι μία λύση απλή σε σκέψη, αλλά πολύπλοκη και χρονοβόρα σε πράξεις και το τελικό αποτέλεσμα, απαιτεί λογισμικό (τουλάχιστον για μένα). Θα την περιγράψω και θα δώσω τον τελικό τύπο του εμβαδού και την απάντηση.
Αν
), γι αυτό και την έλυσα από χτες. Είναι μία λύση απλή σε σκέψη, αλλά πολύπλοκη και χρονοβόρα σε πράξεις και το τελικό αποτέλεσμα, απαιτεί λογισμικό (τουλάχιστον για μένα). Θα την περιγράψω και θα δώσω τον τελικό τύπο του εμβαδού και την απάντηση.
Αν  εύκολα εντοπίζουμε τις άλλες κορυφές και το εμβαδόν δίνεται από τον τύπο:
εύκολα εντοπίζουμε τις άλλες κορυφές και το εμβαδόν δίνεται από τον τύπο: και για
και για  παίρνει μέγιστη τιμή ίση με
παίρνει μέγιστη τιμή ίση με 
Ας δούμε και την παρακάτω.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Ιουν 18, 2018 7:43 pmΓεια σου Γιώργο.Γιώργος Ρίζος έγραψε: ↑Δευ Ιουν 18, 2018 5:37 pmΚαλησπέρα σε όλους.
Ισχύει η γνωστή πρόταση:
Από όλα τα εγγεγραμμένα ν-γωνα σε έναν κύκλο μέγιστο εμβαδόν έχει το κανονικό.
Οπότε το τετράγωνο με διαγώνιες πάνω στους άξονες πληροί τα δεδομένα του προβλήματος κι έχει μέγιστο εμβαδόν ίσο μετ.μ.
Ισχύει η γνωστή πρόταση:
Από όλα τα εγγεγραμμένα ν-γωνα σε έναν κύκλο μέγιστο εμβαδόν έχει το κανονικό.
Υπάρχει στοιχειώδης απόδειξη για αυτό;
Και αν ναι πού είναι;
 τις κεντρικές γωνίες. Αν φέρουμε τις ακτίνες του κύκλου
τις κεντρικές γωνίες. Αν φέρουμε τις ακτίνες του κύκλου  όπου
όπου 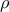 η ακτίνα του περιγεγραμμένου κύκλου.
η ακτίνα του περιγεγραμμένου κύκλου. 
 . Επίσης η
. Επίσης η  είναι κοίλη
είναι κοίλη ![(0,\pi ] (0,\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/1dc6f9287e7af76fbdd2d4b22152c0ec.png) . Από την Jensen τώρα παίρνουμε
. Από την Jensen τώρα παίρνουμε 
 δηλαδή όταν το n-γωνο είναι κανονικό.
δηλαδή όταν το n-γωνο είναι κανονικό. 
Καλημέρα Σταύρο. Το έχω πει πολλές φορές και το ξαναλέω ότι τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 19, 2018 12:38 amΓιώργο καλημέρα.
Γνώριζα ότι υπάρχει απόδειξη αλλά δεν ήξερα καμία.
Τα παραπάνω τα σκέφθηκα.
Συγκεκριμένα είναι γεωμετρικά φανερό (όπως αναλυτικά έδειξες και εσύ)
ότι από τα τρίγωνα με σταθερή βάση που είναι εγγεγραμμένα σε ένα κύκλο
μέγιστο εμβαδό έχει το ισοσκελές.
Αν λοιπόν έχουμε ν-γωνο εγγεγραμμένο σε κύκλο με μέγιστο εμβαδό
τότε αναγκαστικά αυτό θα είναι το κανονικό.
Πράγματι, διαβάζοντας την αγγλική έκδοση του βιβλίου του Tikhomirov, βλέπουμε ότι διαπραγματεύεται ακριβώς αυτόν τον προβληματισμό, αναφερόμενος σε ν-γωνα σταθερής περιμέτρου, και καταλήγει με αρκετά εύληπτο τρόπο στη διατύπωση του ισοπεριμετρικού προβλήματος.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 19, 2018 12:38 am
Το πρόβλημα μου ήταν να αποδείξω ότι υπάρχει ν-γωνο με μέγιστο εμβαδό.
Αυτό μπορεί να προκύψει χρησιμοποιώντας συμπάγεια.
Μου φάνηκε πολύ βαρύ.
Γιαυτό σε ρώτησα.
 .
.Γιώργο καλησπέραΓιώργος Ρίζος έγραψε: ↑Τρί Ιουν 19, 2018 1:09 pmΚαλημέρα Σταύρο. Το έχω πει πολλές φορές και το ξαναλέω ότι τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 19, 2018 12:38 amΓιώργο καλημέρα.
Γνώριζα ότι υπάρχει απόδειξη αλλά δεν ήξερα καμία.
Τα παραπάνω τα σκέφθηκα.
Συγκεκριμένα είναι γεωμετρικά φανερό (όπως αναλυτικά έδειξες και εσύ)
ότι από τα τρίγωνα με σταθερή βάση που είναι εγγεγραμμένα σε ένα κύκλο
μέγιστο εμβαδό έχει το ισοσκελές.
Αν λοιπόν έχουμε ν-γωνο εγγεγραμμένο σε κύκλο με μέγιστο εμβαδό
τότε αναγκαστικά αυτό θα είναι το κανονικό.έχει τη μοναδικότητα να μη δίνει "μασημένη τροφή", π.χ. έτοιμα πακέτα ασκήσεων για κάθε χρήση, αλλά να γεννά αφορμές για αναζητήσεις και έρευνα.
Πράγματι, διαβάζοντας την αγγλική έκδοση του βιβλίου του Tikhomirov, βλέπουμε ότι διαπραγματεύεται ακριβώς αυτόν τον προβληματισμό, αναφερόμενος σε ν-γωνα σταθερής περιμέτρου, και καταλήγει με αρκετά εύληπτο τρόπο στη διατύπωση του ισοπεριμετρικού προβλήματος.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 19, 2018 12:38 am
Το πρόβλημα μου ήταν να αποδείξω ότι υπάρχει ν-γωνο με μέγιστο εμβαδό.
Αυτό μπορεί να προκύψει χρησιμοποιώντας συμπάγεια.
Μου φάνηκε πολύ βαρύ.
Γιαυτό σε ρώτησα.
Το συγκεκριμένο στιγμιότυπο που παρουσίασα παραπάνω, αναφέρεται σε ν-γωνα εγγεγραμμένα σε κύκλο κι όχι σε ισοπεριμετρικά, οπότε νομίζω ότι η απόδειξη δεν έχει πρόβλημα. Προφανώς υπάρχει ν-γωνο εγγεγραμμένο σε δοσμένο κύκλο, για κάθε τιμή του ν μεγαλύτερη του.
Βλέποντας απ' την άλλη την διαφορετική απόδειξη της Αρτέμιδος Καμούδη ΕΔΩ, μού δημιουργούνται αμφιβολίες για την πληρότητα της παραπάνω προσέγγισης.
Θα αναζητήσω σχετικά στοιχεία και στις εργασίες για το ισοπεριμετρικό πρόβλημα των Μ. Λάμπρου- Μ. Κατσοπρινάκη στον Ευκλείδη Γ΄και του Π. Πάμφιλλου στον Θεαίτητο του Μανώλη Μαραγκάκη.
edit: Η εργασία των Μ. Λάμπρου- Μ. Κατσοπρινάκη είναι ΕΔΩ.
 .''
.''Σταύρο καλησπέρα. Δίχως να επιμένω γιατί το θέμα κάθε άλλο παρά προφανές είναι, θέλω να παρατηρήσω ότι αναφέρομαι σε ν-γωνο, άρα η διαδικασία δεν επαναλαμβάνεται άπειρες φορές, αλλά ν μείον μία.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιουν 19, 2018 7:07 pm
Εχει πρόβλημα .Το πρόβλημα είναι ότι η διαδικασία γίνεται άπειρες φορές .Πρέπει λοιπόν να αποδειχθεί ότι η ακολουθία συγκλίνει
στο κανονικό ν-γωνο.
Το ίδιο πρόβλημα υπάρχει και στην απόδειξη της Αρτέμιδος Καμούδη .
Για να πεισθεί κάποιος αρκεί να κάνει την διαδικασία σε ένα τρίγωνο.
Δεν είναι τυχαίο ότι και Tikhomirov παραλείπει την απόδειξη ότι υπάρχει ν-γωνο
με μέγιστο εμβαδό.
Η εκτίμηση μου είναι ότι δεν παίζει ρόλο αν το θεωρήσουμε εγγεγραμμένο η με σταθερή περίμετρο.
 δίνεται η απόδειξη της ύπαρξης του μέγιστου ν-γώνου με την οριακή διαδικασία που περιγράφει ο κ.Σταύρος παραπάνω. Που είναι ειδική περίπτωση του θεωρήματος μέγιστης ελάχιστης τιμής του Weierstrass όπως χαρακτηριστικά αναφέρει ο συγραφέας στο τέλος της απόδειξης.
δίνεται η απόδειξη της ύπαρξης του μέγιστου ν-γώνου με την οριακή διαδικασία που περιγράφει ο κ.Σταύρος παραπάνω. Που είναι ειδική περίπτωση του θεωρήματος μέγιστης ελάχιστης τιμής του Weierstrass όπως χαρακτηριστικά αναφέρει ο συγραφέας στο τέλος της απόδειξης. Είχα χθες " ανεβάσει" μια λάθος λύση θεωρώντας ότι και στην περίπτωση που οι
 είναι παράλληλες στους άξονες , πάλι οι κάθετες διαγώνιοι
είναι παράλληλες στους άξονες , πάλι οι κάθετες διαγώνιοι  για την υπόδειξη .
για την υπόδειξη . και
και  του πολυγώνου δεν ήταν ίσες, θα μπορούσαμε να αυξήσουμε την επιφάνεια του τριγώνου που ορίζουν αυτές οι δύο πλευρές και η διαγώνιος
του πολυγώνου δεν ήταν ίσες, θα μπορούσαμε να αυξήσουμε την επιφάνεια του τριγώνου που ορίζουν αυτές οι δύο πλευρές και η διαγώνιος  λαμβάνοντας ως κορυφή το μέσο του τόξου
λαμβάνοντας ως κορυφή το μέσο του τόξου  . Είναι, επομένως, ίσες οι δύο διαδοχικές χορδές του μεγίστου πολυγώνου, οπότε αυτό είναι το κανονικό.
. Είναι, επομένως, ίσες οι δύο διαδοχικές χορδές του μεγίστου πολυγώνου, οπότε αυτό είναι το κανονικό. με όλες τις πλευρές ίσες εκτός από δύο διαδοχικές
με όλες τις πλευρές ίσες εκτός από δύο διαδοχικές  , τότε αντικαθιστώντας το
, τότε αντικαθιστώντας το  με το μέσο
με το μέσο  του τόξου
του τόξου  , πετυχαίνουμε μεγαλύτερο εμβαδό από το αρχικό. Και υπονοούν ότι αν το αρχικό δεν είχε τις υπόλοιπες πλευρές ίσες, τότε εφαρμόζοντας την ίδια τακτική διαδοχικά σε όλα τα τόξα πετυχαίνουμε το μέγιστο. Τότε όμως, μετακινώντας διαδοχικά τα
, πετυχαίνουμε μεγαλύτερο εμβαδό από το αρχικό. Και υπονοούν ότι αν το αρχικό δεν είχε τις υπόλοιπες πλευρές ίσες, τότε εφαρμόζοντας την ίδια τακτική διαδοχικά σε όλα τα τόξα πετυχαίνουμε το μέγιστο. Τότε όμως, μετακινώντας διαδοχικά τα  όταν φτάσουμε στο τελευταίο τόξο, θα πρέπει να μετακινήσουμε το
όταν φτάσουμε στο τελευταίο τόξο, θα πρέπει να μετακινήσουμε το  και ξεκινάμε από την αρχή...
και ξεκινάμε από την αρχή...  .
. 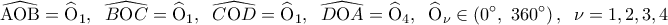 .
.
 με το ίσον μόνον όταν
με το ίσον μόνον όταν  , δηλαδή όταν το τετράπλευρο είναι τετράγωνο.
, δηλαδή όταν το τετράπλευρο είναι τετράγωνο. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες