Δεν είμαι βέβαιος αν κατανόησα την εκφώνηση. Γράφω κάποιες ιδέες για να συζητηθεί το θέμα.

- 26-06-2018 Γεωμετρία 1.png (32.47 KiB) Προβλήθηκε 492 φορές
A) Αν το

συμπέσει με το

τα δύο ορθογώνια ταυτίζονται.
Αν το

συμπέσει με το

, τότε

(γνωστή πρόταση γεωμετρίας Α Λυκείου ή και Γυμνασίου).
Β) Έστω

και

Τότε

άρα

. Τέμνει την

στο

.
Για να είναι εσωτερικό το

στο

πρέπει

Το τριώνυμο έχει Διακρίνουσα

.
Αν είναι

η ανίσωση ισχύει για κάθε τιμή του t στο διάστημα

.
Αν είναι

, τότε το τριώνυμο έχει μια ρίζα

, οπότε αν

, τότε και τα δύο σημεία είναι εσωτερικά των πλευρών

και

.
Αν είναι

η Διακρίνουσα είναι θετική, οπότε

.
Στα διαστήματα αυτά και τα δύο σημεία είναι εσωτερικά των πλευρών

και

.
Γ) Αν ισχύει το (Β), είναι

.
Είναι

, αφού έχουν την ίδια βάση

και
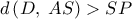
, οπότε

.
Δ) Είναι

.
Είναι

.
Παρατηρώ ότι όταν το

τείνει στο

, τότε το εμβαδό τείνει στο

.
Δεν βλέπω να έχει ελάχιστο το εμβαδό.
 και
και  , ορθογωνίου
, ορθογωνίου  , διαστάσεων
, διαστάσεων  , θεωρούμε
, θεωρούμε ώστε :
ώστε :  και σχεδιάζουμε το ορθογώνιο
και σχεδιάζουμε το ορθογώνιο  .
.  συμπέσει με το
συμπέσει με το  , ή το
, ή το  με το
με το  , είναι :
, είναι : 
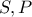 να είναι εσωτερικά σημεία των πλευρών , βρείτε σχέση μεταξύ των
να είναι εσωτερικά σημεία των πλευρών , βρείτε σχέση μεταξύ των  .
. .
. .
.
 (γνωστή πρόταση γεωμετρίας Α Λυκείου ή και Γυμνασίου).
(γνωστή πρόταση γεωμετρίας Α Λυκείου ή και Γυμνασίου). και
και 
 άρα
άρα  . Τέμνει την
. Τέμνει την  στο
στο  .
. πρέπει
πρέπει 
 .
.  η ανίσωση ισχύει για κάθε τιμή του t στο διάστημα
η ανίσωση ισχύει για κάθε τιμή του t στο διάστημα  .
. , τότε το τριώνυμο έχει μια ρίζα
, τότε το τριώνυμο έχει μια ρίζα  , οπότε αν
, οπότε αν  , τότε και τα δύο σημεία είναι εσωτερικά των πλευρών
, τότε και τα δύο σημεία είναι εσωτερικά των πλευρών  η Διακρίνουσα είναι θετική, οπότε
η Διακρίνουσα είναι θετική, οπότε  .
. .
. , αφού έχουν την ίδια βάση
, αφού έχουν την ίδια βάση  και
και  , οπότε
, οπότε  .
. .
. .
. τείνει στο
τείνει στο  , τότε το εμβαδό τείνει στο
, τότε το εμβαδό τείνει στο  .
. . Τότε ασφαλώς αφού για τις δύο οριακές θέσεις των
. Τότε ασφαλώς αφού για τις δύο οριακές θέσεις των  και ενδιάμεσα γίνεται μικρότερο , θα παίρνει και μια
και ενδιάμεσα γίνεται μικρότερο , θα παίρνει και μια
 .
. ,
,  .
. , οπότε με τη βοήθεια της μελέτης του προσήμου του τριωνύμου
, οπότε με τη βοήθεια της μελέτης του προσήμου του τριωνύμου  για
για  ,
,  είναι αύξουσα στο
είναι αύξουσα στο  και φθίνουσα στο
και φθίνουσα στο  ,
,  .
. , οπότε το απόλυτό της έχει ελάχιστο στο
, οπότε το απόλυτό της έχει ελάχιστο στο  .
.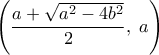 , είδαμε ότι δεν έχει ελάχιστο.
, είδαμε ότι δεν έχει ελάχιστο. , η διακρίνουσα της παραγώγου
, η διακρίνουσα της παραγώγου  ως την ελάχιστη
ως την ελάχιστη  .
.