Πυθαγόρεια κατασκευή

Al.Koutsouridis · #1

Στις πλευρές ορθογωνίου τριγώνου και εξωτερικά αυτού κατασκευάστηκαν τετράγωνα (το γνωστό σχήμα/κατασκευή του Πυθαγόρειου θεωρήματος). Να κατασκευάσετε άλλο ένα τετράγωνο έτσι, ώστε να διαιρεί το καθένα από τα τρία τετράγωνα του Πυθαγόρειου θεωρήματος σε δυο ισοδύναμα μέρη.

#2

Όντως κατασκευάσιμο το τετράγωνο, αφού η λύση προέρχεται από δευτεροβάθμια -- ΠΩΣ όμως;

[Παραθέτω παράδειγμα ελαφρά διορθωμένο -- βλέπετε συζήτηση παρακάτω!]

: πυθαγόρεια-κατασκευή.png (12.63 KiB) Προβλήθηκε 990 φορές

Al.Koutsouridis · #3

gbaloglou έγραψε: ↑
Κυρ Αύγ 26, 2018 6:28 pm
Όντως κατασκευάσιμο το τετράγωνο, αφού η λύση προέρχεται από δευτεροβάθμια -- ΠΩΣ όμως;

πυθαγόρεια-κατασκευή.png

Καλησπέρα κ.Γιώργο,

Το πρόβλημα ίσως να είναι για μεγαλύτερο φάκελο και να μην είναι κατάλληλο για διαγωνισμό λόγω ενδεχομένως πολλών πράξεων. Παρόλα αυτά νομίζω είναι μια όμορφη μη "τυπική" κατασκευή που συνδιάζει πολύπλευρο κομμάτι της ύλης της Β' Λυκείου. Άλλωστε στο σπίτι "έχουμε" χρόνο να ασχοληθούμε όσο θέλουμε

.

#4

Al.Koutsouridis έγραψε: ↑
Κυρ Αύγ 26, 2018 7:51 pm

gbaloglou έγραψε: ↑
Κυρ Αύγ 26, 2018 6:28 pm
Όντως κατασκευάσιμο το τετράγωνο, αφού η λύση προέρχεται από δευτεροβάθμια -- ΠΩΣ όμως;

πυθαγόρεια-κατασκευή.png
Καλησπέρα κ.Γιώργο,

Το πρόβλημα ίσως να είναι για μεγαλύτερο φάκελο και να μην είναι κατάλληλο για διαγωνισμό λόγω ενδεχομένως πολλών πράξεων. Παρόλα αυτά νομίζω είναι μια όμορφη μη "τυπική" κατασκευή που συνδιάζει πολύπλευρο κομμάτι της ύλης της Β' Λυκείου. Άλλωστε στο σπίτι "έχουμε" χρόνο να ασχοληθούμε όσο θέλουμε .

Αλέξανδρε είναι ένα πολύ όμορφο πρόβλημα, θα δώσω τον τύπο που έβγαλα αν δεν ασχοληθεί κάποιος άλλος. Θα μπορούσα να το μετακινήσω και στον 'φάκελλο καθηγητή' που επιμελούμαι ("Γεωμετρία"), ας μείνει όμως εδώ προς το παρόν μήπως και έχει κάποιος έμπνευση και δώσει γεωμετρική κατασκευή! (Όπως πάντως είδαμε και εδώ προ διετίας, η κατασκευασιμότητα δεν οδηγεί αυτόματα σε (κομψή) γεωμετρική κατασκευή...)

Ας πω επίσης ότι στην αρχή ζητούσα λύση με 'πλάγιο' τετράγωνο του οποίου οι τρεις πλευρές διέρχονται από τα κέντρα των τριών τετραγώνων, κάτι που μάλλον δεν είναι εφικτό -- μου μπήκαν ψύλλοι στ' αυτιά όταν δοκίμασα την περίπτωση ισοσκελούς ορθογωνίου

Made in Russia η ομιχλώδης κατασκευή;

#5

Καλησπέρα σε όλους. Επιχειρώ μια υπολογιστική προσέγγιση σε ένα συγκεκριμένο τρίγωνο, με γνωστές συντεταγμένες. Δεν τολμώ να επεκταθώ στη γενίκευση αντικαθιστώντας τα B(6,0), C(0,8)

με

. Άλλωστε είναι ακόμα Αύγουστος!

: 26-08-2018 Γεωμετρία.png (52.23 KiB) Προβλήθηκε 1046 φορές

Παίρνουμε μια ειδική περίπτωση. Το τρίγωνο ABC

με

και το τετράγωνο MNPL

με $\displaystyle {\rm M}\left( { - 4,\; - 3} \right),\;N\left( {a,\; - 3} \right),\;P\left( {a,\;a + 1} \right),\;L\left( { - 4,\;a + 1} \right)$ , με 8< a < 14

που προφανώς χωρίζει τα τετράγωνα ACDE, ABHZ

σε ίσα μέρη.

Έστω ότι χωρίζει και το BCKI

σε δύο ισοδύναμα μέρη.

Είναι $\displaystyle CK:\;\;y = \frac{3}{4}x + 8$ , άρα $\displaystyle R\left( {\frac{{4\left( {a - 7} \right)}}{3},\;a + 1} \right)$ και Y(0, a+1)

.
Οπότε $\displaystyle \left( {CYR} \right) = \frac{1}{2}CY \cdot YR = \frac{1}{2} \cdot \left( {a - 7} \right)\frac{{4\left( {a - 7} \right)}}{3} = \frac{{2{{\left( {a - 7} \right)}^2}}}{3}$

Είναι $\displaystyle BI:\;\;y = \frac{3}{4}x - \frac{{18}}{4}$ , άρα $\displaystyle S\left( {a,\frac{{3\left( {a - 6} \right)}}{4}} \right)$ και Χ(a,0)

.

Οπότε $\displaystyle \left( {BSX} \right) = \frac{1}{2}BX \cdot SX = \frac{1}{2} \cdot \left( {a - 6} \right)\frac{{3\left( {a - 6} \right)}}{4} = \frac{{3{{\left( {a - 6} \right)}^2}}}{8}$

Τότε $\displaystyle \left( {CRPSB} \right) = \left( {AXPY} \right) - \left( {CYR} \right) - \left( {BSX} \right) - \left( {ABC} \right) = a\left( {a + 1} \right) - \frac{{2{{\left( {a - 7} \right)}^2}}}{3} - \frac{{3{{\left( {a - 6} \right)}^2}}}{8} - 24$ .

Και αφού $\displaystyle \left( {CRPSB} \right) = \frac{{\left( {BCKI} \right)}}{2} = 50$ , προκύπτει η εξίσωση $\displaystyle {a^2} - 356a + 2884 = 0$

που δίνει δεκτή ρίζα $\displaystyle a = \frac{{356 - \sqrt {{{356}^2} - 4 \cdot 2884} }}{2} \simeq 8,29$ .

edit: Είναι προφανές ότι η ιδέα του σχήματος ανήκει στον συνονόματο Γιώργο Μπαλόγλου, όπως την αποτύπωσε στο προηγούμενο σχήμα.

Al.Koutsouridis · #6

Ο κ.Μπαλόγλου μάντεψε σωστά και ως αναφορά σε ποιο φάκελο θα έπρεπε να είναι το πρόβλημα κανονικά αλλά και την πηγή.

Το θέμα είναι απο περσινό διαγωνισμό για δασκάλους (καθηγητές) στη Ρωσία με την ονομασία "Δημιουργικός διαγωνισμός για δασκάλους". Χωρίζεται σε τρία μέρη, λύση προβλημάτων, μεθοδολογία και παιδαγωγική. Το παραπάνω πρόβλημα είναι από το πρώτο μέρος λύση προβλημάτων.

Ως αναφορά την ειδική περίπτωση του κ.Ρίζου παραπάνω με κάθετες πλευρές 6,8

, να σημειώσουμε ότι αν οι κάθετες πλευρές διαφέρουν σχετικά λίγο, μπορούν να βρεθούν πολύ απλές κατασκευές. Παρ' όλα αυτά η σύνθεση παραμένει κοπιαστική.

#7

Al.Koutsouridis έγραψε: ↑
Δευ Αύγ 27, 2018 11:05 am
Ο κ.Μπαλόγλου μάντεψε σωστά και ως αναφορά σε ποιο φάκελο θα έπρεπε να είναι το πρόβλημα κανονικά αλλά και την πηγή.

Το θέμα είναι απο περσινό διαγωνισμό για δασκάλους (καθηγητές) στη Ρωσία με την ονομασία "Δημιουργικός διαγωνισμός για δασκάλους". Χωρίζεται σε τρία μέρη, λύση προβλημάτων, μεθοδολογία και παιδαγωγική. Το παραπάνω πρόβλημα είναι από το πρώτο μέρος λύση προβλημάτων.

Ως αναφορά την ειδική περίπτωση του κ.Ρίζου παραπάνω με κάθετες πλευρές , να σημειώσουμε ότι αν οι κάθετες πλευρές διαφέρουν σχετικά λίγο, μπορούν να βρεθούν πολύ απλές κατασκευές. Παρ' όλα αυτά η σύνθεση παραμένει κοπιαστική.

Πολύ ενδιαφέροντα όλα αυτά, Αλέξανδρε, ας επισημάνω εδώ ότι ο άλλος Γιώργος εργάστηκε ουσιαστικά στο ίδιο παράδειγμα με μένα ... και ότι οι απαντήσεις μας διαφέρουν λίγο, με την δική μου να είναι η εσφαλμένη: δεν κατάφερα προς το παρόν να βρω το λαθάκι στον γενικό τύπο μου, θα επανέλθω το απόγευμα

#8

gbaloglou έγραψε: ↑
Δευ Αύγ 27, 2018 11:16 am

Al.Koutsouridis έγραψε: ↑
Δευ Αύγ 27, 2018 11:05 am
Ο κ.Μπαλόγλου μάντεψε σωστά και ως αναφορά σε ποιο φάκελο θα έπρεπε να είναι το πρόβλημα κανονικά αλλά και την πηγή.

Το θέμα είναι απο περσινό διαγωνισμό για δασκάλους (καθηγητές) στη Ρωσία με την ονομασία "Δημιουργικός διαγωνισμός για δασκάλους". Χωρίζεται σε τρία μέρη, λύση προβλημάτων, μεθοδολογία και παιδαγωγική. Το παραπάνω πρόβλημα είναι από το πρώτο μέρος λύση προβλημάτων.

Ως αναφορά την ειδική περίπτωση του κ.Ρίζου παραπάνω με κάθετες πλευρές , να σημειώσουμε ότι αν οι κάθετες πλευρές διαφέρουν σχετικά λίγο, μπορούν να βρεθούν πολύ απλές κατασκευές. Παρ' όλα αυτά η σύνθεση παραμένει κοπιαστική.
Πολύ ενδιαφέροντα όλα αυτά, Αλέξανδρε, ας επισημάνω εδώ ότι ο άλλος Γιώργος εργάστηκε ουσιαστικά στο ίδιο παράδειγμα με μένα ... και ότι οι απαντήσεις μας διαφέρουν λίγο, με την δική μου να είναι η εσφαλμένη: δεν κατάφερα προς το παρόν να βρω το λαθάκι στον γενικό τύπο μου, θα επανέλθω το απόγευμα

Παραθέτω την γενική λύση -- που επαληθεύει και το αποτέλεσμα του Γιώργου Ρίζου -- στο συνημμένο: όλα έπονται από τον υπολογισμό του x, μικρότερη λύση της δευτεροβάθμιας που προκύπτει από την εξίσωση του ημιεμβαδού του τρίτου (και μεγαλύτερου) τετραγώνου προς το εμβαδόν του τέταρτου (και διχοτομούντος) τετραγώνου μείον τα εμβαδά των έξι αριθμημένων χωρίων.

Το συνημμένο μπορεί να δοθεί και σε μαθητές (αν θέλουμε να κάνουμε την άσκηση πιο προσιτή).

#9

Για τον εορταζόμενο Αλέξανδρο, αλλά και για όλους τους άλλους ... ένα σχήμα 'με το μάτι':

: τριμεσοτετράγωνο.png (7.76 KiB) Προβλήθηκε 862 φορές

Al.Koutsouridis · #10

gbaloglou έγραψε: ↑
Παρ Αύγ 31, 2018 12:35 am
Για τον εορταζόμενο Αλέξανδρο, αλλά και για όλους τους άλλους ... ένα σχήμα 'με το μάτι':

τριμεσοτετράγωνο.png

Ευχαριστώ για τις ευχές κ.Γιώργο,

Προσπάθησα να προσδιορίσω ποιό ορθογώνιο τρίγωνο επιδέχεται τέτοια κατασκευή. Πήγα με αναλυτική γεωμετρία και κατέληξα σε σύστημα τριών εξισώσεων δευτέρου βαθμού αλλά δεν κατάφερα να το λύσω και το παράτησα

.

Παραθέτω όμως για προυλαρισμό μια απλή κατασκευή (όχι δική μου, από την πηγή που άντλησα το θέμα) που "δουλεύει" για κάποια ορθογώνια τρίγωνα με συγκεκριμένο εύρος τιμών του λόγου των κάθετων πλευρών του.

: puthagoreia_kataskeyh.png (17.38 KiB) Προβλήθηκε 797 φορές

#11

Al.Koutsouridis έγραψε: ↑
Κυρ Σεπ 02, 2018 12:07 pm

gbaloglou έγραψε: ↑
Παρ Αύγ 31, 2018 12:35 am
Για τον εορταζόμενο Αλέξανδρο, αλλά και για όλους τους άλλους ... ένα σχήμα 'με το μάτι':

τριμεσοτετράγωνο.png
Ευχαριστώ για τις ευχές κ.Γιώργο,

Προσπάθησα να προσδιορίσω ποιό ορθογώνιο τρίγωνο επιδέχεται τέτοια κατασκευή. Πήγα με αναλυτική γεωμετρία και κατέληξα σε σύστημα τριών εξισώσεων δευτέρου βαθμού αλλά δεν κατάφερα να το λύσω και το παράτησα .

Έχω αποδείξει ότι ΔΕΝ γίνεται για το τρίγωνο 3-4-5 και πιστεύω ότι η μέθοδος μου μπορεί τελικά να επεκταθεί σε ΟΛΑ τα ορθογώνια τρίγωνα ... υπάρχουν όμως πλέον άλλες προτεραιότητες (βλέπε παρακάτω)

Παραθέτω όμως για προυλαρισμό μια απλή κατασκευή (όχι δική μου, από την πηγή που άντλησα το θέμα) που "δουλεύει" για κάποια ορθογώνια τρίγωνα με συγκεκριμένο εύρος τιμών του λόγου των κάθετων πλευρών του.

Αλέξανδρε υπονοείς ότι η πηγή σου ΔΕΝ δίνει λύση για όλες τις περιπτώσεις;! Έχω αποδείξει ότι η αρχική μου λύση, ειδική περίπτωση αυτής που παρέθεσες, ισχύει για ΟΛΑ τα ορθογώνια τρίγωνα (και θα δώσω τις λεπτομέρειες αργότερα, αφού βέβαια τις ελέγξω).

puthagoreia_kataskeyh.png

Al.Koutsouridis · #12

gbaloglou έγραψε: ↑
Δευ Σεπ 03, 2018 9:18 am

Αλέξανδρε υπονοείς ότι η πηγή σου ΔΕΝ δίνει λύση για όλες τις περιπτώσεις;! Έχω αποδείξει ότι η αρχική μου λύση, ειδική περίπτωση αυτής που παρέθεσες, ισχύει για ΟΛΑ τα ορθογώνια τρίγωνα (και θα δώσω τις λεπτομέρειες αργότερα, αφού βέβαια τις ελέγξω).

Όχι μάλλον δεν το έγραψα καθαρά. Μία από τις επίσημες λύσεις είναι παρόμοια με την δική σας, απλά λαμβάνει ως

την λευρά του τετραγώνου προς κατασκευή και προκύπτει η πιό συμμετρική σχέση

$\displaystyle x =\dfrac{a^3}{(a-b)^2} + \dfrac{b^3}{(a-b)^2} -\dfrac{ab\sqrt{2a^2+2b^2}}{(a-b)^2}$

και όπως σωστά αναφέρατε υπάρχει (αποδεικνύεται) πάντα τέτοια κατασκευή. (τετράγωνο με πλευρές παράλληλες προς τις καθέτους).

Ως αναφορά το σχήμα (κατασκευή) που παρουσίασα παραπάνω στη #10 δημοσίευση. Πλαγιαστό τετράγωνο με πλευρές παράλληλες στις διαγωνίους του τετραγώνου της υποτείνουσας και με κορυφή στο μέσο της απόστασης μεταξύ του κέντρου του τετραγώνου της υποτείνουσας και της πλευράς απέναντι αυτής. Αυτή είναι μια πολύ απλή κατασκευή και αποδεικνύεται σχετικά εύκολα ότι είναι η ζητούμενη. Μια καλή άσκηση παρεμπιπτόντως.

Το μειονέκτημα είναι, ότι δουλεύει αν οι κορυφές του τετραγώνου προς κατασκευή δεν πέφτουν μέσα στα τετράγωνα του Πυθαγορείου θεωρήματος. Αποδεικνύεται ότι αυτό γίνεται για λόγο κάθετων πλευρών $\displaystyle t=\dfrac{CB}{CA} \in \left [ 1, r\right ]$ . Όπου

, η ρίζα της εξίσωσης $\displaystyle t^3-t^2-t-1 = 0$ .

Υπάρχει και μια δέυτερη λύση/κατασκευή που δίνεται στη πηγή και είναι αρκετά διδακτική νομίζω. Θα προσπαθήσω να την παρουσιάσω κάποια άλλη στιγμή.

Τα παραπάνω καθώς και τα θέματα άλλων ετών μπορούν να βρεθούν στη σελίδα του διαγωνισμού.

#13

Al.Koutsouridis έγραψε: ↑
Δευ Σεπ 03, 2018 12:34 pm

gbaloglou έγραψε: ↑
Δευ Σεπ 03, 2018 9:18 am

Αλέξανδρε υπονοείς ότι η πηγή σου ΔΕΝ δίνει λύση για όλες τις περιπτώσεις;! Έχω αποδείξει ότι η αρχική μου λύση, ειδική περίπτωση αυτής που παρέθεσες, ισχύει για ΟΛΑ τα ορθογώνια τρίγωνα (και θα δώσω τις λεπτομέρειες αργότερα, αφού βέβαια τις ελέγξω).

Όχι μάλλον δεν το έγραψα καθαρά. Μία από τις επίσημες λύσεις είναι παρόμοια με την δική σας, απλά λαμβάνει ως την λευρά του τετραγώνου προς κατασκευή και προκύπτει η πιό συμμετρική σχέση

$\displaystyle x =\dfrac{a^3}{(a-b)^2} + \dfrac{b^3}{(a-b)^2} -\dfrac{ab\sqrt{2a^2+2b^2}}{(a-b)^2}$

και όπως σωστά αναφέρατε υπάρχει (αποδεικνύεται) πάντα τέτοια κατασκευή. (τετράγωνο με πλευρές παράλληλες προς τις καθέτους).

Καταθέτω τις λεπτομέρειες της προσέγγισης μου (for whatever it's worth, που λέγαμε και στο χωριό μου)...

Αρχίζοντας με τις δύο παράλληλες προς τις καθέτους πλευρές, διερχόμενες δια των κέντρων των αντίστοιχων τετραγώνων, επεκτείνουμε αρχικά την μικρότερη κατά $\dfrac{b-a}{2}$ σχηματίζοντας ένα 'αρχικό' τετράγωνο (κατά το ήμισυ), και εν συνεχεία επεκτείνουμε αμφότερες τις πλευρές κατά

(βλέπετε συνημμένο) ... ώστε να επιδιωχθεί το ζητούμενο: προκύπτει, από την εξίσωση του εμβαδού έξι χωρίων προς το ημιεμβαδόν του τρίτου τετραγώνου όπως είχα γράψει εξ αρχής (βλ. τέταρτη μου δημοσίευση), μία δευτεροβάθμια ως προς

που μας δίνει την σωστή του τιμή, $x=\dfrac{a(a^2+3b^2)-2\sqrt{2}ab\sqrt{a^2+b^2}}{2(b-a)^2}$ .

Εύκολα προκύπτει τώρα ότι η τέταρτη κορυφή του ζητούμενου τετραγώνου είναι η $(\dfrac{a}{2}+\dfrac{b}{2}+x, b+x)$ , το ερώτημα είναι αν οφείλει ΟΝΤΩΣ να βρίσκεται ΕΝΤΟΣ του τρίτου τετραγώνου, ώστε να έχει νόημα η όλη στρατηγική και λύση (βλ. συνημμένο): προτίμησα να αντιμετωπίσω αυτό το ερώτημα αλγεβρικά, αποδεικνύοντας ότι η απόσταση της τέταρτης κορυφής από κάθε μία από τις πλευρές του τρίτου τετραγώνου δεν υπερβαίνει το μήκος της πλευράς του ( $c=\sqrt{a^2+b^2}$ )^ δίνω τις βασικές λεπτομέρειες παρακάτω, πλευρά προς πλευρά.

--

: $\dfrac{b}{a}x+y-b=0$ , με αντίστοιχη ανισότητα απόστασης τέταρτης κορυφής αναγόμενη στην

$(a+b)\dfrac{|(a^2+b^2)(a+b)-2\sqrt{2}ab\sqrt{a^2+b^2}|}{2(b-a)^2}\leq a^2+b^2.$

Η απόλυτη τιμή μπορεί να αφαιρεθεί χάρις στην $(b-a)^2(b^2+4ab+a^2)\geq 0$ , οπότε η ζητούμενη ανισότητα ανάγεται στην

$(a^2+b^2)(6ab-a^2-b^2)\leq 2\sqrt{2}ab(a+b)\sqrt{a^2+b^2}.$

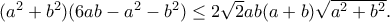
Η ανισότητα αυτή ισχύει τετριμμένα αν $6ab-a^2-b^2\leq 0$ , στην αντίθετη περίπτωση θέτουμε b=ra

(με $r\geq 1$ , r^2+1<6r

) και, ύστερα από ύψωση στο τετράγωνο, καταλήγουμε σε μία ανισότητα ισοδύναμη προς την

$(r-1)^2(r^4-10r^3+10r^2-10r+1)\leq 0,$

που ισχύει λόγω r^4-10r^3+10r^2-10r+1<-4r^3+10r^2-10r=-r(4r^2-10r+10)<0

. (Η

δίνει $r^4-6r^3+1\leq r^4-6r^3+r^2<0$ .)

--

: $\dfrac{a}{b}x-y+b=0$ , με αντίστοιχη ανισότητα απόστασης τέταρτης κορυφής αναγόμενη στην

$\dfrac{|-a(a^2+b^2)+\sqrt{2}ab\sqrt{a^2+b^2}|}{b-a}\leq a^2+b^2,$

που ανάγεται εύκολα στην $\sqrt{2}a\leq \sqrt{a^2+b^2}$ .

--

: $\dfrac{b}{a}x+y-a-b-\dfrac{b^2}{a}=0$ , με αντίστοιχη ανισότητα απόστασης τέταρτης κορυφής αναγόμενη στην

$\dfrac{|6a^3b+4ab^3-a^4-a^2b^2-2\sqrt{2}ab(a+b)\sqrt{a^2+b^2}|}{2(b-a)^2}\leq a^2+b^2.$

Η απόλυτη τιμή μπορεί να αφαιρεθεί χάρις στην $a^2(b-a)^3(8b^3+9a^2b-a^3)\geq 0$ , οπότε η ζητούμενη ανισότητα ανάγεται, ύστερα από χρήση των $a+b\geq 2\sqrt{ab}$ , $\sqrt{a^2+b^2}\geq \sqrt{2}\sqrt{ab}$ , στην ισχύουσα $(b-a)^2(2b^2-4ab+3a^2)\geq 0$ .

--

: $\dfrac{a}{b}x-y-\dfrac{a^2}{b}=0$ , με αντίστοιχη ανισότητα απόστασης τέταρτης κορυφής αναγόμενη στην

$\dfrac{|-b(a^2+b^2)+\sqrt{2}ab\sqrt{a^2+b^2}|}{b-a}\leq a^2+b^2,$

που ανάγεται εύκολα στην $\sqrt{a^2+b^2}\leq \sqrt{2}b$ .

: fourth-bisecting-square-proof.png (22.33 KiB) Προβλήθηκε 707 φορές

#14

Al.Koutsouridis έγραψε: ↑
Κυρ Σεπ 02, 2018 12:07 pm

gbaloglou έγραψε: ↑
Παρ Αύγ 31, 2018 12:35 am
Για τον εορταζόμενο Αλέξανδρο, αλλά και για όλους τους άλλους ... ένα σχήμα 'με το μάτι':

τριμεσοτετράγωνο.png
Ευχαριστώ για τις ευχές κ.Γιώργο,

Προσπάθησα να προσδιορίσω ποιό ορθογώνιο τρίγωνο επιδέχεται τέτοια κατασκευή. Πήγα με αναλυτική γεωμετρία και κατέληξα σε σύστημα τριών εξισώσεων δευτέρου βαθμού αλλά δεν κατάφερα να το λύσω και το παράτησα .

Τελικά, ενάντια στην αρχική μου διαίσθηση και τις μέχρι τέλους ελπίδες ... ΔΕΝ γίνεται

Η στρατηγική μου συνοψίζεται στο συνημμένο: χρησιμοποιώντας ως μεταβλητή τον συντελεστή διεύθυνσης

των δύο πλευρών του αναζητούμενου τετραγώνου ... εκφράζουμε τις τομές τους

,

με τις 'πάνω' πλευρές των αντίστοιχων τετραγώνων ΚΑΙ τις δύο 'κάτω' κορυφές

,

του αναζητούμενου τετραγώνου συναρτήσει του

: για να υπάρχει πράγματι το αναζητούμενο τετράγωνο οφείλουν να ισχύουν οι $|PQ|\leq |QR|$ , $|SR|\leq |QR|$ ... έτσι ώστε να μπορούν να επεκταθούν οι δύο πλευρές (φορείς των

,

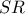) μέχρις ότου εξισωθούν προς την ήδη γνωστή πλευρά

και να 'κλείσει' το τετράγωνο^ αυτές οι δύο ανισότητες ΔΕΝ μπορούν όμως να ισχύουν ταυτόχρονα (όπως αναφέρω στο συνημμένο, παραλείποντας τις τριωνυμικές λεπτομέρειες*).

*η $|PQ|\leq |QR|$ ανάγεται στην $|(a+2b)r^2-(a+b)r+b|\leq |(a+2b)r^2-ar|$ , που δίνει, για $r\geq \dfrac{a}{a+2b}$ (μόνη δυνατή περίπτωση), $r\geq 1$ , ενώ η $|SR|\leq |QR|$ ανάγεται στην $|(2b^2+2ab+a^2)r^2+(b^2-ab-2a^2)r+(b^2-ab+a^2)|\leq |(2b^2+ab)r^2-(a^2+3b)r+a^2|$ , που δίνει, για $r\leq \dfrac{a}{a+2b}$ (μόνη δυνατή περίπτωση), $-\dfrac{b}{a}\leq r\leq -\dfrac{b-a}{a+b}$ .

: r-3-squares.png (42.65 KiB) Προβλήθηκε 654 φορές

Πυθαγόρεια κατασκευή

Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Re: Πυθαγόρεια κατασκευή

Μέλη σε σύνδεση