 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  Στον ίδιο κύκλο εγγράφουμε τρίγωνο
Στον ίδιο κύκλο εγγράφουμε τρίγωνο 
με
 Αν
Αν  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  να δείξετε ότι
να δείξετε ότι 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  Στον ίδιο κύκλο εγγράφουμε τρίγωνο
Στον ίδιο κύκλο εγγράφουμε τρίγωνο 
 Αν
Αν  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  να δείξετε ότι
να δείξετε ότι 
 που προφανώς είναι μεσοκάθετος στις
που προφανώς είναι μεσοκάθετος στις  και έστω
και έστω  το σημείο τομής της με την
το σημείο τομής της με την  .
. θα είναι
θα είναι  και
και 

 και κόψει την
και κόψει την  στο
στο  ομοίως έχω
ομοίως έχω  δηλαδή η διαγώνιος
δηλαδή η διαγώνιος  του παραλληλογράμμου
του παραλληλογράμμου  είναι κάθετη στην
είναι κάθετη στην  .
. είναι ισόπλευρο και αναγκαστικά το παραλληλόγραμμο
είναι ισόπλευρο και αναγκαστικά το παραλληλόγραμμο  είναι ρόμβος άρα
είναι ρόμβος άρα  .
. τέμνουν τον κύκλο στα
τέμνουν τον κύκλο στα  αντίστοιχα,προκύπτει ότι
αντίστοιχα,προκύπτει ότι  κάθετες στην
κάθετες στην  .(απλό κυνήγι γωνιών-φαίνεται και από την παραπάνω λύση).Άρα η πολική του
.(απλό κυνήγι γωνιών-φαίνεται και από την παραπάνω λύση).Άρα η πολική του  περνάει από το (σταθερό) σημείο στο άπειρο με προσανατολισμό κάθετο στην
περνάει από το (σταθερό) σημείο στο άπειρο με προσανατολισμό κάθετο στην  ,και επειδή ισχύει το αντίθετο και επιπλέον οι πολικές των σημείων στο άπειρο περνούν από το
,και επειδή ισχύει το αντίθετο και επιπλέον οι πολικές των σημείων στο άπειρο περνούν από το  ,το
,το  κινείται σε ευθεία.Όμως,αν
κινείται σε ευθεία.Όμως,αν  το σημείο στο άπειρο,πρέπει
το σημείο στο άπειρο,πρέπει  ,
, κάθετες,όμως εξ'ορισμού του
κάθετες,όμως εξ'ορισμού του  είναι
είναι  κάθετες και το ζητούμενο έπεται...
κάθετες και το ζητούμενο έπεται...Χωρίς βλάβη της γενικότητας θεωρούμε το δοσμένο κύκλο ως το μοναδιαίο και το σημείοgeorge visvikis έγραψε: ↑Τετ Αύγ 29, 2018 10:08 amΙσόπλευρο και παραλληλία.png
Ισόπλευρο τρίγωνοείναι εγγεγραμμένο σε κύκλο κέντρου
Στον ίδιο κύκλο εγγράφουμε τρίγωνο

μεΑν
είναι το ορθόκεντρο του τριγώνου
να δείξετε ότι

 να συμπίπτει με την φανταστική μονάδα (
να συμπίπτει με την φανταστική μονάδα ( ).
). του ορθόκεντρου τριγώνου
του ορθόκεντρου τριγώνου  με κορυφές στο μοναδιαίο κύκλο δίνεται από την σχέση
με κορυφές στο μοναδιαίο κύκλο δίνεται από την σχέση  .
. ,
,  σημείων του μοναδιάιου κύκλου έχουμε
σημείων του μοναδιάιου κύκλου έχουμε 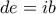 ,
, 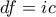 . Οπότε για το ορθόκεντρο έχουμε
. Οπότε για το ορθόκεντρο έχουμε
 βρίσκεται στον πραγματικό άξονα και
βρίσκεται στον πραγματικό άξονα και  .
. και
και 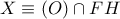 .
.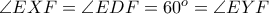 και
και  προκύπτει εύκολα ότι
προκύπτει εύκολα ότι  και
και 
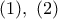 έχουμε ότι το ορθόκεντρο
έχουμε ότι το ορθόκεντρο  του
του  , ταυτίζεται με το σημείο τομής των διαγωνίων του μεταβλητού τραπεζίου
, ταυτίζεται με το σημείο τομής των διαγωνίων του μεταβλητού τραπεζίου  με
με  σταθερής διεύθυνσης.
σταθερής διεύθυνσης. κάθετη ευθεία επί των βάσεων του ως άνω μεταβλητού τραπεζίου περνάει από το κέντρο
κάθετη ευθεία επί των βάσεων του ως άνω μεταβλητού τραπεζίου περνάει από το κέντρο  του κύκλου
του κύκλου  , είναι παράλληλη προς την
, είναι παράλληλη προς την  λόγω των
λόγω των 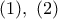 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.george visvikis έγραψε: ↑Τετ Αύγ 29, 2018 10:08 amΙσόπλευρο και παραλληλία.png
Ισόπλευρο τρίγωνοείναι εγγεγραμμένο σε κύκλο κέντρου
Στον ίδιο κύκλο εγγράφουμε τρίγωνο

μεΑν
είναι το ορθόκεντρο του τριγώνου
να δείξετε ότι

 ισοσκελή τραπέζια, θα είναι
ισοσκελή τραπέζια, θα είναι  ισοσκελές τραπέζιο,άρα
ισοσκελές τραπέζιο,άρα ,επομένως και τα αντίστοιχα αποστήματα αυτών
,επομένως και τα αντίστοιχα αποστήματα αυτών  θα είναι ίσα.
θα είναι ίσα. .Ακόμη,
.Ακόμη,  (το συμμετρικό του
(το συμμετρικό του  ως προς
ως προς είναι σημείο του κύκλου)
είναι σημείο του κύκλου)  είναι ισόπλευρο
είναι ισόπλευρο θα είναι
θα είναι  .Αλλά
.Αλλά  ,οπότε
,οπότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες