Γιώργος Μήτσιος έγραψε: ↑Παρ Σεπ 21, 2018 2:12 pm
Χαίρετε. Μια τροποποίηση παλαιού θέματος με την προσδοκία να δούμε και
νέες ιδέες-λύσεις.
Σταθερός λόγος.PNG
Το (σταθερό) τρίγωνο

έχει

, το

είναι το μέσον της

ενώ το
 κινείται
κινείται στην πλευρά

Η μεσοκάθετος του

τέμνει την

στο

και τον περίκυκλο του τριγώνου
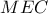
στο

. Στην

παίρνουμε

.
Να εξεταστεί αν ο λόγος  είναι σταθερός.
Εφαρμογή : Αν
είναι σταθερός.
Εφαρμογή : Αν  να βρεθούν οι οξείες γωνίες του
να βρεθούν οι οξείες γωνίες του 
Ευχαριστώ, Γιώργος.
Καλησπέρα σε όλους!

- Σταθερός λόγος.Μ.png (16.56 KiB) Προβλήθηκε 628 φορές
Από το εγγεγραμμένο

και το ισοσκελές

οι πράσινες γωνίες είναι ίσες κι επειδή το

είναι παραλληλόγραμμο,
θα είναι

Αλλά,

και το
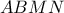
είναι εγγράψιμο, άρα και οι κόκκινες γωνίες είναι ίσες. Οπότε το

είναι εγγράψιμο,

και τα τρίγωνα

είναι όμοια. Άρα:
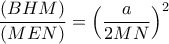
Από την ομοιότητα όμως των τριγώνων

παίρνουμε τελικά:

Αν τώρα

βρίσκουμε

Γιώργος Μήτσιος έγραψε: ↑Παρ Σεπ 21, 2018 10:26 pm
...Ας κάνουμε ( και ..

..όχι άσκοπα) ένα κόπο ακόμη :
Να δειχθεί ότι το τρίγωνο  του σχήματος είναι όμοιο με το
του σχήματος είναι όμοιο με το 
.
Εύκολα τώρα τα τρίγωνα είναι όμοια επειδή είναι ορθογώνια (

, από το εγγράψιμο

) και έχουν τις κόκκινες γωνίες ίσες.
 έχει
έχει  , το
, το  είναι το μέσον της
είναι το μέσον της  ενώ το
ενώ το  κινείται στην πλευρά
κινείται στην πλευρά 
 τέμνει την
τέμνει την  στο
στο  και τον περίκυκλο του τριγώνου
και τον περίκυκλο του τριγώνου 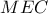 στο
στο  . Στην
. Στην  παίρνουμε
παίρνουμε  .
. είναι σταθερός.
είναι σταθερός. να βρεθούν οι οξείες γωνίες του
να βρεθούν οι οξείες γωνίες του 

 που τις τέμνουν στα
που τις τέμνουν στα  αντίστοιχα. Προφανώς
αντίστοιχα. Προφανώς 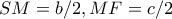 και
και  (βλέπουν το ίδιο τόξο στον κύκλο).
(βλέπουν το ίδιο τόξο στον κύκλο).
 έχουμε
έχουμε  . Αρα
. Αρα  και
και 
 του σχήματος είναι
του σχήματος είναι  είναι μεσοκάθετος της
είναι μεσοκάθετος της  .
. παραλληλόγραμμο. Αρα
παραλληλόγραμμο. Αρα  .
. είναι εγγράψιμο γιατί η
είναι εγγράψιμο γιατί η  φαίνεται από τις κορυφές
φαίνεται από τις κορυφές  υπό ίσες γωνίες μέτρου
υπό ίσες γωνίες μέτρου  . Αρα κοι η
. Αρα κοι η  φαίνεται από τις
φαίνεται από τις  υπό ίσες γωνίες συγκεκριμένα μέτρου
υπό ίσες γωνίες συγκεκριμένα μέτρου  .
. έχει δύο γωνίες
έχει δύο γωνίες  ίσες με του
ίσες με του  άρα είναι όμοια.
άρα είναι όμοια. και το ισοσκελές
και το ισοσκελές  οι πράσινες γωνίες είναι ίσες κι επειδή το
οι πράσινες γωνίες είναι ίσες κι επειδή το  είναι παραλληλόγραμμο,
είναι παραλληλόγραμμο,  Αλλά,
Αλλά,  και το
και το 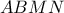 είναι εγγράψιμο, άρα και οι κόκκινες γωνίες είναι ίσες. Οπότε το
είναι εγγράψιμο, άρα και οι κόκκινες γωνίες είναι ίσες. Οπότε το είναι εγγράψιμο,
είναι εγγράψιμο,  και τα τρίγωνα
και τα τρίγωνα  είναι όμοια. Άρα:
είναι όμοια. Άρα: 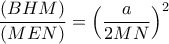
 παίρνουμε τελικά:
παίρνουμε τελικά: 
 βρίσκουμε
βρίσκουμε 
 , από το εγγράψιμο
, από το εγγράψιμο  στο
στο 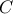 τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  .
. ορθογώνιο θα είναι
ορθογώνιο θα είναι  παραλ/μμο ,επομένως η
παραλ/μμο ,επομένως η 
 και
και  μεσοκάθετος της
μεσοκάθετος της 
 οι μαύρες γωνίες είναι ίσες όπως και οι μωβ οπότε
οι μαύρες γωνίες είναι ίσες όπως και οι μωβ οπότε 

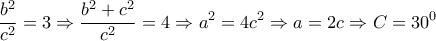 και
και 