 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  . Έστω σημεία
. Έστω σημεία  των πλευρών
των πλευρών  για τα οποία
για τα οποία  .
.Ας είναι
 το κέντρο του κύκλου
το κέντρο του κύκλου  . Δείξετε ότι η διάκεντρος
. Δείξετε ότι η διάκεντρος  είναι παράλληλη στη διχοτόμος
είναι παράλληλη στη διχοτόμος  του τριγώνου
του τριγώνου  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  . Έστω σημεία
. Έστω σημεία  των πλευρών
των πλευρών  για τα οποία
για τα οποία  .
. το κέντρο του κύκλου
το κέντρο του κύκλου  . Δείξετε ότι η διάκεντρος
. Δείξετε ότι η διάκεντρος  είναι παράλληλη στη διχοτόμος
είναι παράλληλη στη διχοτόμος  του τριγώνου
του τριγώνου  .
.Οι μεσοκάθετοι των
 τέμνονται στο
τέμνονται στο  Τα τρίγωνα
Τα τρίγωνα  είναι προφανώς ίσα (Π-Π-Π), άρα οι μπλε γωνίες
είναι προφανώς ίσα (Π-Π-Π), άρα οι μπλε γωνίες είναι κοινό σημείο των δύο κύκλων. Επειδή η
είναι κοινό σημείο των δύο κύκλων. Επειδή η  είναι διάμετρος
είναι διάμετρος 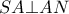 , αλλά
, αλλά  (η διάκεντρος είναι κάθετη στην κοινή χορδή). Επομένως
(η διάκεντρος είναι κάθετη στην κοινή χορδή). Επομένως 
 και
και  ενός σκαληνού τριγώνου
ενός σκαληνού τριγώνου  , θεωρούμε αντίστοιχα τα σημεία
, θεωρούμε αντίστοιχα τα σημεία  και
και  .
.  είναι το μέσο του τόξου
είναι το μέσο του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  .
.  ισχύει, αν και μόνο αν τα σημεία
ισχύει, αν και μόνο αν τα σημεία  ,
,  ,
,  ,
,  είναι ομοκυκλικά.
είναι ομοκυκλικά. και
και  είναι ίσα, εφόσον
είναι ίσα, εφόσον  ,
,  , και
, και 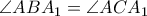 .
. 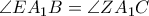 . Επομένως
. Επομένως  .
. τέμνει τον περιγεγραμμένο κύκλο
τέμνει τον περιγεγραμμένο κύκλο  του
του  στο σημείο
στο σημείο 
 που δεν περιέχει την κορυφή
που δεν περιέχει την κορυφή  , δηλαδή,
, δηλαδή,  .
.  είναι τετράπλευρο του οποίου οι διαγώνιοί του τέμνονται κάθετα στο σημείο
είναι τετράπλευρο του οποίου οι διαγώνιοί του τέμνονται κάθετα στο σημείο 
 , δηλαδή, η
, δηλαδή, η  διάμετρος του
διάμετρος του  .
. είναι το μέσο του τόξου
είναι το μέσο του τόξου  του κύκλου
του κύκλου  , δηλαδή
, δηλαδή  .
.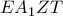 είναι τετράπλευρο του οποίου οι διαγώνιοί του τέμνονται κάθετα στο σημείο
είναι τετράπλευρο του οποίου οι διαγώνιοί του τέμνονται κάθετα στο σημείο 
 , δηλαδή, η
, δηλαδή, η  διάμετρος του
διάμετρος του  (από την απόδειξη του λήμματος,
(από την απόδειξη του λήμματος,  είναι ισοσκελές με τη γωνία της κορυφής του να ισούται με τη γωνία
είναι ισοσκελές με τη γωνία της κορυφής του να ισούται με τη γωνία  ).
).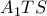 , είναι φανερό ότι
, είναι φανερό ότι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: KARKAR και 14 επισκέπτες