Ο έγκυκλος κέντρου
 , τριγώνου
, τριγώνου  εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα.Η ευθεία
 τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  και την ευθεία
και την ευθεία  στο
στο  .
.Αν
 το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 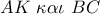 δείξετε ότι :
δείξετε ότι : 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , τριγώνου
, τριγώνου  εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα. τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  και την ευθεία
και την ευθεία  στο
στο  .
. το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 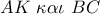 δείξετε ότι :
δείξετε ότι : 
Καλημέρα κ. Νίκο !
 είναι το μέσον της
είναι το μέσον της  .
. το σημείο Gergonne του τριγώνου (το σημείο
το σημείο Gergonne του τριγώνου (το σημείο  είναι το σημείο συντρέχειας των
είναι το σημείο συντρέχειας των  ). Από το πλήρες
). Από το πλήρες  έχω ότι τα
έχω ότι τα  είναι αρμονικά συζυγή.
είναι αρμονικά συζυγή. .
. και
και 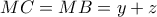 .
. ή ισοδύναμα
ή ισοδύναμα  , και αφού
, και αφού  (αν
(αν  , άτοπο) είναι
, άτοπο) είναι  .
. .
. και προκύπτει
και προκύπτει  , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε. και θέτω
και θέτω 
 μέσο του
μέσο του  .Έστω
.Έστω  η ημιπερίμετρος του
η ημιπερίμετρος του 
 με διατέμνουσα
με διατέμνουσα  έχουμε
έχουμε 
 που ισχύει .
που ισχύει . παράλληλη στην
παράλληλη στην  που τέμνει τις
που τέμνει τις  στα
στα  αντίστοιχα.Αρκεί
αντίστοιχα.Αρκεί  μέσον του
μέσον του  .
. και
και  εγγράψιμα και προκύπτει εύκολα
εγγράψιμα και προκύπτει εύκολα  δηλαδή
δηλαδή  ισοσκελές άρα
ισοσκελές άρα  ύψος και διάμεσος....
ύψος και διάμεσος....Η πολική του
 ως προς τον έγκυκλο είναι προφανώς η
ως προς τον έγκυκλο είναι προφανώς η  ( χορδή των επαφών) που διέρχεται από το
( χορδή των επαφών) που διέρχεται από το  .
.  ως προς τον ίδιο κύκλο θα διέρχεται από το
ως προς τον ίδιο κύκλο θα διέρχεται από το  , αλλά κι από το
, αλλά κι από το  γιατί το
γιατί το  είναι εφαπτόμενο τμήμα , δηλαδή είναι η
είναι εφαπτόμενο τμήμα , δηλαδή είναι η  .
.  , κόψει την
, κόψει την  στο
στο  τότε η δέσμη:
τότε η δέσμη:  είναι αρμονική και επομένως η τετράδα
είναι αρμονική και επομένως η τετράδα  είναι αρμονική.
είναι αρμονική. είναι μέσο του
είναι μέσο του  όπως πολύ σωστά ανέφεραν πιο πάνω οι φερέλπιδες νέοι Ορέστης και Πρόδρομος .
όπως πολύ σωστά ανέφεραν πιο πάνω οι φερέλπιδες νέοι Ορέστης και Πρόδρομος . που η
που η  το τέμνει στο σημείο
το τέμνει στο σημείο  και αφού
και αφού  είναι αρμονική το
είναι αρμονική το  είναι εφαπτόμενο τμήμα στο ημικύκλιο
είναι εφαπτόμενο τμήμα στο ημικύκλιο  είναι διχοτόμος του
είναι διχοτόμος του  . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  με ύψος προς την υποτείνουσα
με ύψος προς την υποτείνουσα  και λόγω του Θ. διχοτόμου στο
και λόγω του Θ. διχοτόμου στο  έχω:
έχω: 
Καλησπέρα!
 είναι αρμονική (εύκολο) και
είναι αρμονική (εύκολο) και  μέσο του
μέσο του  ,άρα από
,άρα από  έχω :
έχω :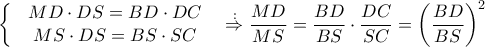
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες