 είναι ορθογώνιο και ισοσκελές . Σημείο
είναι ορθογώνιο και ισοσκελές . Σημείο  βρίσκεται "αριστερά" της
βρίσκεται "αριστερά" της 
και είναι τέτοιο ώστε :
 και
και  . Ονομάζω
. Ονομάζω  την τομή των
την τομή των 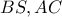
και
 τη διχοτόμο της
τη διχοτόμο της  . α) Υπολογίστε το λόγο :
. α) Υπολογίστε το λόγο :  ... β) Δείξτε ότι :
... β) Δείξτε ότι :  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι ορθογώνιο και ισοσκελές . Σημείο
είναι ορθογώνιο και ισοσκελές . Σημείο  βρίσκεται "αριστερά" της
βρίσκεται "αριστερά" της 
 και
και  . Ονομάζω
. Ονομάζω  την τομή των
την τομή των 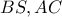
 τη διχοτόμο της
τη διχοτόμο της  . α) Υπολογίστε το λόγο :
. α) Υπολογίστε το λόγο :  ... β) Δείξτε ότι :
... β) Δείξτε ότι :  .
.
 .
. είναι όμοια, άρα:
είναι όμοια, άρα:
 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  .Με διάμετρο
.Με διάμετρο  γράψω το ημικύκλιο
γράψω το ημικύκλιο 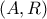 που περιέχει το
που περιέχει το  . Ας είναι
. Ας είναι  το σημείο τομής της ημιευθείας
το σημείο τομής της ημιευθείας  μ αυτό .
μ αυτό .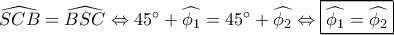 .
.  και άρα το
και άρα το 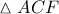 είναι ισόπλευρο .
είναι ισόπλευρο .  και
και 
 έχω την εξίσωση :
έχω την εξίσωση : 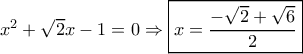
 και η
και η  διχοτόμος του
διχοτόμος του 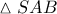 θα ισχύουν:
θα ισχύουν: 
 το μέσο του
το μέσο του  Είναι
Είναι 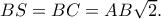 Από
Από  α) Νόμος συνημιτόνων στο
α) Νόμος συνημιτόνων στο 


 Επίσης είναι
Επίσης είναι  (οι διχοτόμοι των εντός εναλλάξ
(οι διχοτόμοι των εντός εναλλάξ  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  Από την προφανή τώρα ισότητα
Από την προφανή τώρα ισότητα  προκύπτει το ζητούμενο
προκύπτει το ζητούμενο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες