KARKAR έγραψε: ↑Τετ Δεκ 18, 2019 1:07 pm
Μέσος και λόγος.pngΜε σημείο

διαιρούμε το τμήμα

σε δύο τμήματα

και

.
Σχεδιάζουμε στο ίδιο ημιεπίπεδο τα ισόπλευρα τρίγωνα

και

.
Τα τμήματα

τέμνονται στο σημείο

.
α) Δείξτε ότι το τμήμα

είναι ο γεωμετρικός μέσος των

.
β) Δείξτε ότι :

. Πότε θα έχουμε :

;
Θεωρώ

το σημείο τομής της

με τον περίκυκλο του

και θα δείξω ότι τα σημεία

είναι συνευθειακά.
Πράγματι,

άρα και το

είναι εγγράψιμο κι επειδή

τα

είναι συνευθειακά, οπότε

είναι το σημείο τομής των


- Μέσος και λόγος.Κ.png (23.24 KiB) Προβλήθηκε 371 φορές
α) Από τα δύο εγγράψιμα τετράπλευρα και από τις προφανείς παραλληλίες

και

οι κόκκινες
γωνίες είναι ίσες, όπως και οι μπλε. Άρα τα τρίγωνα

είναι όμοια, απ' όπου

β) Οι

εφάπτονται στους κύκλους

αντίστοιχα.

και ομοίως

Άρα,


με την ισότητα να ισχύει όταν

Για

εύκολα προκύπτει ότι

ή

 διαιρούμε το τμήμα
διαιρούμε το τμήμα  σε δύο τμήματα
σε δύο τμήματα  και
και  .
. και
και  .
.  τέμνονται στο σημείο
τέμνονται στο σημείο  .
. είναι ο γεωμετρικός μέσος των
είναι ο γεωμετρικός μέσος των  .
. . Πότε θα έχουμε :
. Πότε θα έχουμε :  ;
;
 όμοια
όμοια που ισχύει και
που ισχύει και  όταν
όταν  ή
ή 
 και
και  άρα οι πράσινες
άρα οι πράσινες  εγγράψιμα .
εγγράψιμα . τέμνει την
τέμνει την  στο
στο 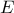 και προφανώς
και προφανώς  και
και 

 και
και  και με πολ/σμό έχουμε
και με πολ/σμό έχουμε
 και
και  και με πολ/σμό
και με πολ/σμό ή
ή  με τον περίκυκλο του
με τον περίκυκλο του  είναι συνευθειακά.
είναι συνευθειακά.  άρα και το
άρα και το  είναι εγγράψιμο κι επειδή
είναι εγγράψιμο κι επειδή  τα
τα 
 και
και  οι κόκκινες
οι κόκκινες 
 εφάπτονται στους κύκλους
εφάπτονται στους κύκλους  αντίστοιχα.
αντίστοιχα. και ομοίως
και ομοίως 

 με την ισότητα να ισχύει όταν
με την ισότητα να ισχύει όταν 
 εύκολα προκύπτει ότι
εύκολα προκύπτει ότι  ή
ή 
 άρας γωνίας
άρας γωνίας  .
. . Συνεπώς :
. Συνεπώς : 