Μέγιστη διχοτόμος

#1

: Μέγιστη διχοτόμος.png (16 KiB) Προβλήθηκε 777 φορές

Σε ημικύκλιο διαμέτρου AOB=2R

επιλέγουμε σημείο

έτσι ώστε αν

είναι οποιοδήποτε σημείο του τόξου $\overset\frown{AC},$ να

ισχύει $A\widehat DC=A\widehat OC.$ Να κατασκευάσετε το σχήμα και να βρείτε τη μέγιστη τιμή της διχοτόμου

του τριγώνου DAC.

ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ · #2

Γεια σας κ.Γιώργο

Για την κατασκευή του

:
Θα είναι $\omega =\widehat{ABC}=\dfrac{\widehat{AOC}}{2}=\dfrac{\widehat{ADC}}{2}$ . Όμως $\widehat{ABC}+\widehat{ADC}=180^{\circ}\Leftrightarrow 3\omega= 180^{\circ}\Leftrightarrow \omega =60^{\circ}$ .
Έτσι λοιπόν $C\equiv (O,R)\cap (B,BO)$ .

Απο το

φέρω κάθετη στην

, που τέμνει αυτήν και το ημικύκλιο στα

και

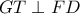αντίστοιχα. Φέρω ακόμη $GT\perp FD$ . Λόγω συμμετρίας, θεωρώ πως $D\in \overset{\frown }{FC}$ . Η

και

είναι η εσωτερική και η εξωτερική διχοτόμος, αντίστοιχα, της γωνίας $\widehat{ADC}$ , έτσι $DF\perp DE$ . Επιπλέον εαν $M\equiv FD\cap GE$ , είναι $\dfrac{GT}{ED}=\dfrac{MT}{MD}\geq 1$ , με την ισότητα να ισχύει όταν $T\equiv F$ , οπότε $FD\parallel GC$ , δηλαδή

είναι το επάπειρον σημείο των ευθειών. Έτσι προκύπτει $DE\leq GT\leq GF=R/2$ .

: Μέγιστη διχοτόμος.png (46.81 KiB) Προβλήθηκε 737 φορές

#3

α) Ας είναι

το μέσο της χορδής

. Επειδή: $2\widehat {{\theta _{}}} = \widehat {ADC} = 180^\circ - \widehat {{\theta _{}}} \Rightarrow \widehat {{\theta _{}}} = 60^\circ$ .

Το

λοιπόν θα είναι το σημείο επαφής της από το

εφαπτομένης στον κύκλο : $\boxed{\left( {O,r = \frac{R}{2}} \right)}$ ,

: Μέγιστη διχοτόμος.png (31.04 KiB) Προβλήθηκε 691 φορές

β) Σε κάθε $\vartriangle ABC$ έχω: $h \leqslant d \leqslant m$ με h,d,m

: ύψος, διχοτόμος και διάμεσος από την ίδια κορυφή .

Εδώ θα έχω μέγιστη διχοτόμο όταν $\boxed{d = m = \frac{R}{2}}$ δηλαδή το

θα είναι το

συμμετρικό του

ως προς το

και το τετράπλευρο ADCO

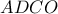γίνει ρόμβος.

Μέγιστη διχοτόμος

Μέγιστη διχοτόμος

Re: Μέγιστη διχοτόμος

Re: Μέγιστη διχοτόμος

Μέλη σε σύνδεση