Σελίδα 1 από 1
Σταθερό σημείο και γωνία
Δημοσιεύτηκε: Παρ Νοέμ 20, 2020 7:23 pm
από KARKAR

- Σταθερότητα σημείου και γωνία.png (12.58 KiB) Προβλήθηκε 471 φορές
Σε τρίγωνο

, θεωρούμε σημείο

της

, ώστε

. Σημείο

κινείται
στην

και ας ονομάσουμε

την τομή των

και

την τομή των

.
α) Δείξτε ότι η ευθεία

διέρχεται από σταθερό σημείο , ας το πούμε

.
β) Αν :
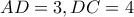
, για ποια θέση του

, είναι :

;
Re: Σταθερό σημείο και γωνία
Δημοσιεύτηκε: Παρ Νοέμ 20, 2020 9:40 pm
από S.E.Louridas
Η απόκρυψη θα γίνει μετά από επόμενη διαπραγμάτευση:
α) Είναι το αρμονικό συζυγές

του

ως προς τα

από το πλήρες τετράπλευρο

β) είναι τομή της

με τόξο που βλέπει τo

με γωνία
 edit:
edit: Άρση της απόκρυψης μετά την άριστη ανάρτηση του Νίκου.
Re: Σταθερό σημείο και γωνία
Δημοσιεύτηκε: Σάβ Νοέμ 21, 2020 3:12 am
από Doloros
α) Ας είναι το σημείο τομής των

. Θα δείξω ότι το

είναι το ζητούμενο .
Η ευθεία

-Πάππου για τις τριάδες των σημείων :

διέρχεται από το

και τα σημεία

που τέμνονται τα ζεύγη των ευθειών:

αντίστοιχα.

- Σταθερό σημείο και γωνία_oritzin_a.png (33.86 KiB) Προβλήθηκε 420 φορές
Άμεση συνέπεια : Οι πολικές και του

αλλά και του

ταυτίζονται με την ευθεία

. ( Κατασκευή πολικής )
Η ευθεία αυτή τέμνει την

στο

και η τετράδα:

είναι αρμονική οπότε και η τετράδα
είναι αρμονική,
Αν λοιπόν θέσω

κι επειδή :

και άρα το

σταθερό .
β)

- Σταθερό σημείο και γωνία_oritzin_b.png (25 KiB) Προβλήθηκε 420 φορές
Επιλέγω :

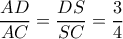
και άρα η

διχοτόμος του

.

 Το α ερώτημα πιθανόν να προκύπτει με Θ . Μενελάου και Θ.
Το α ερώτημα πιθανόν να προκύπτει με Θ . Μενελάου και Θ. 
 , θεωρούμε σημείο
, θεωρούμε σημείο  της
της  , ώστε
, ώστε  . Σημείο
. Σημείο  κινείται
κινείται και ας ονομάσουμε
και ας ονομάσουμε  την τομή των
την τομή των  και
και  την τομή των
την τομή των  .
. διέρχεται από σταθερό σημείο , ας το πούμε
διέρχεται από σταθερό σημείο , ας το πούμε  .
.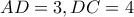 , για ποια θέση του
, για ποια θέση του  , είναι :
, είναι :  ;
; , θεωρούμε σημείο
, θεωρούμε σημείο  της
της  , ώστε
, ώστε  . Σημείο
. Σημείο  κινείται
κινείται και ας ονομάσουμε
και ας ονομάσουμε  την τομή των
την τομή των  και
και  την τομή των
την τομή των  .
. διέρχεται από σταθερό σημείο , ας το πούμε
διέρχεται από σταθερό σημείο , ας το πούμε  .
.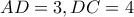 , για ποια θέση του
, για ποια θέση του  , είναι :
, είναι :  ;
; από το πλήρες τετράπλευρο
από το πλήρες τετράπλευρο 
 με γωνία
με γωνία 
 . Θα δείξω ότι το
. Θα δείξω ότι το  -Πάππου για τις τριάδες των σημείων :
-Πάππου για τις τριάδες των σημείων : 
 και τα σημεία
και τα σημεία  που τέμνονται τα ζεύγη των ευθειών:
που τέμνονται τα ζεύγη των ευθειών:  αντίστοιχα.
αντίστοιχα. ταυτίζονται με την ευθεία
ταυτίζονται με την ευθεία  . ( Κατασκευή πολικής )
. ( Κατασκευή πολικής ) στο
στο  και η τετράδα:
και η τετράδα:  είναι αρμονική οπότε και η τετράδα
είναι αρμονική οπότε και η τετράδα  είναι αρμονική,
είναι αρμονική, κι επειδή :
κι επειδή :  και άρα το
και άρα το 
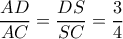 και άρα η
και άρα η  διχοτόμος του
διχοτόμος του  .
. 

