gbaloglou έγραψε: ↑Σάβ Μάιος 15, 2021 11:24 am
Ως ελάχιστη δική μου συνεισφορά, ιδού ένα ακέραιο, μη ισόπλευρο 'συνευθειακό' τρίγωνο με ακόμη μικρότερη περίμετρο: {

}.
Ξεκινώντας από το παραπάνω, ας βρούμε και το τρίγωνο με την ελάχιστη περίμετρο (σκιαγράφηση):
Χρησιμοποιώντας την μέθοδο του Νίκου, βρίσκουμε ότι τα ζητούμενα τρίγωνα είναι της μορφής {

}. Από τις ανισότητες

του Νίκου προκύπτει ότι η περίμετρος είναι τουλάχιστον ίση προς

, και επειδή παραπάνω έχουμε ήδη περίμετρο

... συμπεραίνουμε ότι για ενδεχομένως μικρότερη περίμετρο οφείλει να ισχύει η

.
Επειδή οι

δεν έχουν κοινό διαιρέτη, συμπεραίνουμε ότι o

οφείλει να διαιρεί τον

. Ταυτόχρονα, ο

οφείλει να διαιρεί τον

. Δοκιμάζοντας τις διάφορες τιμές

και περιορίζοντας αντίστοιχα τις δυνατές τιμές του

μέσω

βλέπουμε ότι 'γρήγορα' αρχίζουν να χάνονται οι ελπίδες για την

: δεν το πήγα μέχρι τέλους, σταμάτησα στην
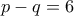
, αλλά βρίσκω μία λύση για

, δύο λύσεις για

, μία λύση για

, καμία λύση για

, μία λύση για
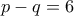
. Οι λύσεις αυτές είναι οι εξής:

-- τρίγωνο {

}
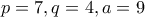
-- τρίγωνο {
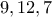
}

-- τρίγωνο {

}

-- τρίγωνο {

}
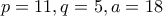
-- τρίγωνο {

}
Τα τελευταία δύο τρίγωνα τα γνωρίζαμε ήδη, αλλά η ελάχιστη δυνατή περίμετρος είναι, με ελάχιστη πιθανότητα λάθους,

.
ΠΡΟΣΘΗΚΗ 16-5-21 7:55 πμ: Καμία πιθανότητα λάθους, καθώς -- πλέον -- η

επιβάλλει

και

: δεν υπάρχουν πλέον 'υποψήφια' τρίγωνα με περίμετρο

. (Ευχαριστώ τον Νίκο Ιωσηφίδη για συζήτηση και μικρές διορθώσεις.)
 είναι σημεία των πλευρών
είναι σημεία των πλευρών  , τριγώνου
, τριγώνου  και τα
και τα  τα συμμετρικά των
τα συμμετρικά των 
 . Είναι γνωστό ότι τα
. Είναι γνωστό ότι τα  είναι συνευθειακά , αν οι
είναι συνευθειακά , αν οι  , είναι διάμεσοι .
, είναι διάμεσοι . είναι : α) ύψη ... β) διχοτόμοι .
είναι : α) ύψη ... β) διχοτόμοι .
 και
και  , οπότε η ζητούμενη συνευθειακότητα είναι ισοδύναμη προς την
, οπότε η ζητούμενη συνευθειακότητα είναι ισοδύναμη προς την  ).
). θα πρέπει να κινείται σε έλλειψη με κέντρο το μέσο της πλευράς
θα πρέπει να κινείται σε έλλειψη με κέντρο το μέσο της πλευράς  , μεγάλο άξονα στο φορέα αυτού του τμήματος και μήκους
, μεγάλο άξονα στο φορέα αυτού του τμήματος και μήκους  , μικρό άξονα μήκους
, μικρό άξονα μήκους  . Δεν δοκίμασα με συντεταγμένες, γεωμετρικά δεν κατέληξα κάπου προς το παρόν.
. Δεν δοκίμασα με συντεταγμένες, γεωμετρικά δεν κατέληξα κάπου προς το παρόν. οι πλευρές του τριγώνου
οι πλευρές του τριγώνου  ισχύει (βλ. Νίκου Ιωσηφίδη (2008),
ισχύει (βλ. Νίκου Ιωσηφίδη (2008),  και
και 
 και
και 
 είναι μέσο του
είναι μέσο του  ισχύει:
ισχύει: 

 συνευθειακά πρέπει και αρκεί να υπάρχει
συνευθειακά πρέπει και αρκεί να υπάρχει 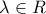 :
:  και, ισοδύναμα λόγω (1) & (2),
και, ισοδύναμα λόγω (1) & (2), 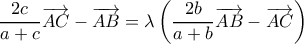 .
.  και
και  είναι γραμμικώς ανεξάρτητα, πρέπει και αρκεί να ισχύουν οι
είναι γραμμικώς ανεξάρτητα, πρέπει και αρκεί να ισχύουν οι 

 από την 1η στην 2η σχέση προκύπτει
από την 1η στην 2η σχέση προκύπτει  να είναι συνευθειακά.
να είναι συνευθειακά. είναι μια ρητή λύση της (3) τότε η τριάδα
είναι μια ρητή λύση της (3) τότε η τριάδα  θα είναι ακέραια λύση της (3). Θεωρούμε ότι οι λύσεις της μορφής
θα είναι ακέραια λύση της (3). Θεωρούμε ότι οι λύσεις της μορφής  , που δίνουν όμοια τρίγωνα είναι ταυτόσημες.
, που δίνουν όμοια τρίγωνα είναι ταυτόσημες. ώστε
ώστε  , οπότε
, οπότε  . Από τις σχέσεις αυτές βρίσκουμε
. Από τις σχέσεις αυτές βρίσκουμε

 που ισχύει για κάθε
που ισχύει για κάθε 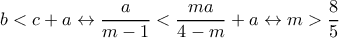

 .
. 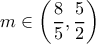 και τυχαίο ρητό
και τυχαίο ρητό  , έχουμε τη ρητή λύση
, έχουμε τη ρητή λύση  .
. και τυχαίο ρητό
και τυχαίο ρητό  .
. έχουμε την ακέραια λύση
έχουμε την ακέραια λύση  .
. ) .
) . }.
}. }. Από τις ανισότητες
}. Από τις ανισότητες  του Νίκου προκύπτει ότι η περίμετρος είναι τουλάχιστον ίση προς
του Νίκου προκύπτει ότι η περίμετρος είναι τουλάχιστον ίση προς  , και επειδή παραπάνω έχουμε ήδη περίμετρο
, και επειδή παραπάνω έχουμε ήδη περίμετρο  ... συμπεραίνουμε ότι για ενδεχομένως μικρότερη περίμετρο οφείλει να ισχύει η
... συμπεραίνουμε ότι για ενδεχομένως μικρότερη περίμετρο οφείλει να ισχύει η  .
.  δεν έχουν κοινό διαιρέτη, συμπεραίνουμε ότι o
δεν έχουν κοινό διαιρέτη, συμπεραίνουμε ότι o  οφείλει να διαιρεί τον
οφείλει να διαιρεί τον  οφείλει να διαιρεί τον
οφείλει να διαιρεί τον  . Δοκιμάζοντας τις διάφορες τιμές
. Δοκιμάζοντας τις διάφορες τιμές  και περιορίζοντας αντίστοιχα τις δυνατές τιμές του
και περιορίζοντας αντίστοιχα τις δυνατές τιμές του  βλέπουμε ότι 'γρήγορα' αρχίζουν να χάνονται οι ελπίδες για την
βλέπουμε ότι 'γρήγορα' αρχίζουν να χάνονται οι ελπίδες για την  : δεν το πήγα μέχρι τέλους, σταμάτησα στην
: δεν το πήγα μέχρι τέλους, σταμάτησα στην 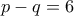 , αλλά βρίσκω μία λύση για
, αλλά βρίσκω μία λύση για  , δύο λύσεις για
, δύο λύσεις για  , μία λύση για
, μία λύση για  , καμία λύση για
, καμία λύση για  , μία λύση για
, μία λύση για  -- τρίγωνο {
-- τρίγωνο { }
}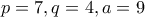 -- τρίγωνο {
-- τρίγωνο {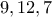 }
} -- τρίγωνο {
-- τρίγωνο { }
}  -- τρίγωνο {
-- τρίγωνο { }
}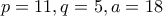 -- τρίγωνο {
-- τρίγωνο { .
. επιβάλλει
επιβάλλει  και
και  : δεν υπάρχουν πλέον 'υποψήφια' τρίγωνα με περίμετρο
: δεν υπάρχουν πλέον 'υποψήφια' τρίγωνα με περίμετρο  συναρτήσει της
συναρτήσει της  , είναι :
, είναι :  .
.