 "επισυνάπτουμε" το ορθογώνιο
"επισυνάπτουμε" το ορθογώνιο  , με το
, με το  στην
στην  ,
,το
 στην προέκταση της
στην προέκταση της  και την πλευρά
και την πλευρά  να διέρχεται από την κορυφή
να διέρχεται από την κορυφή  .
.α) Δείξτε ότι το ορθογώνιο έχει εμβαδόν μεγαλύτερο από εκείνο του τετραγώνου .
β) Αν
 , για ποια θέση του
, για ποια θέση του  , προκύπτει :
, προκύπτει :  ;
;
 , το μισό τετράγωνο είναι το,
, το μισό τετράγωνο είναι το,  και αφού έχουν κοινό το πράσινο χωρίο αρκεί να δείξουμε ότι:
και αφού έχουν κοινό το πράσινο χωρίο αρκεί να δείξουμε ότι:  .
. οπότε αρκεί :
οπότε αρκεί :  που ισχύει .
που ισχύει .  η προβολή του
η προβολή του  και
και  το σημείο τομής των
το σημείο τομής των  . Θέτω :
. Θέτω :  .
.
 έχω:
έχω: 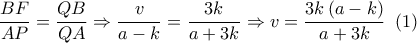
 .
.  ,
,  . Έτσι έχω την εξίσωση :
. Έτσι έχω την εξίσωση :  και το
και το  μέσο του
μέσο του  .
.