Δύο ορθογώνια τρίγωνα
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Δύο ορθογώνια τρίγωνα
Δύο ορθογώνια τρίγωνα έχουν ίδιο το εμβαδόν και ίδια την περίμετρο. Να εξετάσετε αν είναι υποχρεωτικά ίσα .
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Δύο ορθογώνια τρίγωνα
Ναι, είναι ίσα.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Σάβ Ιαν 15, 2022 8:43 pmΔύο ορθογώνια τρίγωνα έχουν ίδιο το εμβαδόν και ίδια την περίμετρο. Να εξετάσετε αν είναι υποχρεωτικά ίσα .
Έστω
 και
και  το κοινό εμβαδόν και η περίμετρος, αντίστοιχα. Aν
το κοινό εμβαδόν και η περίμετρος, αντίστοιχα. Aν  οι κάθετες πλευρές του ενός τριγώνου, έχουμε
οι κάθετες πλευρές του ενός τριγώνου, έχουμε  και
και  . H δεύτερη γράφεται
. H δεύτερη γράφεται  που με ύψωση στο τετράγωνο και με χρήση της πρώτης δίνει
που με ύψωση στο τετράγωνο και με χρήση της πρώτης δίνει 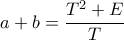
Με άλλα λόγια οι πλευρές ικανοποιούν τις σχέσεις
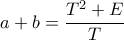 και
και  . Άρα είναι οι ρίζες της
. Άρα είναι οι ρίζες της  .
.Οι κάθετες πλευρές
 οποιουδήποτε άλλου τριγώνου με το ίδιο εμβαδόν και περίμετρο ικανοποιούν ακριβώς την ίδια εξίσωση. Οπότε τελικά οι ρίζες τις ικανοποιούν είτε (
οποιουδήποτε άλλου τριγώνου με το ίδιο εμβαδόν και περίμετρο ικανοποιούν ακριβώς την ίδια εξίσωση. Οπότε τελικά οι ρίζες τις ικανοποιούν είτε (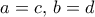 ) ή (
) ή ( ) (ίδια τρίγωνα και στις δύο περιπτώσεις).
) (ίδια τρίγωνα και στις δύο περιπτώσεις).Υπάρχουν και άλλοι τρόποι απόδειξης της ιδιότητας.
-
Μιχάλης Τσουρακάκης
- Δημοσιεύσεις: 2770
- Εγγραφή: Παρ Ιαν 11, 2013 4:17 am
- Τοποθεσία: Ηράκλειο Κρήτης
Re: Δύο ορθογώνια τρίγωνα
Είναι γνωστό ότι στο ορθογώνιο τρίγωνοΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Σάβ Ιαν 15, 2022 8:43 pmΔύο ορθογώνια τρίγωνα έχουν ίδιο το εμβαδόν και ίδια την περίμετρο. Να εξετάσετε αν είναι υποχρεωτικά ίσα .
 είναι
είναι 
Επομένως
 κι επειδή
κι επειδή 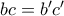 παίρνουμε
παίρνουμε  άρα και
άρα και 
Θεωρούμε τώρα τα ορθογώνια τρίγωνα
 με
με  και
και  οπότε
οπότε 
Ο ν.συνημιτόνου στα τρίγωνα
 δίνει
δίνει και
και
κι επειδή
 καθώς και
καθώς και 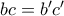 ,εύκολα έχουμε
,εύκολα έχουμε  άρα
άρακαι
 ,συνεπώς
,συνεπώς 
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Δύο ορθογώνια τρίγωνα
Ας δούμε και μια λύση ακόμα:
Επειδή το εμβαδόν κάθε τριγώνου δίνεται από τον τύπο , έπεται άμεσα ότι τα δύο ορθογώνια τρίγωνα έχουν ίδια την ακτίνα
, έπεται άμεσα ότι τα δύο ορθογώνια τρίγωνα έχουν ίδια την ακτίνα  του εγγεγραμμένου τους κύκλου. Άρα οι κάθετες πλευρές στο ένα τρίγωνο θα είναι
του εγγεγραμμένου τους κύκλου. Άρα οι κάθετες πλευρές στο ένα τρίγωνο θα είναι  και στο άλλο
και στο άλλο 
Από την υπόθεση, έχουμε: και άρα
και άρα  (1)
(1)
Από το Πυθαγόρειο θεώρημα στα δύο τρίγωνα έχουμε:


Μετά τις απλές πράξεις έχουμε:


Οπότε λόγω και της (1) έχουμε (2)
(2)
Από την (1) τώρα έχουμε: και λόγω της (2), θα είναι
και λόγω της (2), θα είναι  (3)
(3)
Από τις (1) και (3) έχουμε:


Άρα:

 .(4)
.(4)
Αν είναι , τότε θα είναι και
, τότε θα είναι και  και προφανώς τα ορθογώνια τρίγωνα είναι ίσα
και προφανώς τα ορθογώνια τρίγωνα είναι ίσα
Αν είναι , τότε θα είναι και
, τότε θα είναι και  και η (4) μας δίνει
και η (4) μας δίνει  . Συνεπώς έχουμε το σύστημα:
. Συνεπώς έχουμε το σύστημα:


Με πρόσθεση κατά μέλη παίρνουμε: και με αφαίρεση
και με αφαίρεση  , οπότε και πάλι τα τρίγωνα είναι ίσα
, οπότε και πάλι τα τρίγωνα είναι ίσα
Επειδή το εμβαδόν κάθε τριγώνου δίνεται από τον τύπο
 , έπεται άμεσα ότι τα δύο ορθογώνια τρίγωνα έχουν ίδια την ακτίνα
, έπεται άμεσα ότι τα δύο ορθογώνια τρίγωνα έχουν ίδια την ακτίνα  του εγγεγραμμένου τους κύκλου. Άρα οι κάθετες πλευρές στο ένα τρίγωνο θα είναι
του εγγεγραμμένου τους κύκλου. Άρα οι κάθετες πλευρές στο ένα τρίγωνο θα είναι  και στο άλλο
και στο άλλο 
Από την υπόθεση, έχουμε:
 και άρα
και άρα  (1)
(1)Από το Πυθαγόρειο θεώρημα στα δύο τρίγωνα έχουμε:


Μετά τις απλές πράξεις έχουμε:


Οπότε λόγω και της (1) έχουμε
 (2)
(2)Από την (1) τώρα έχουμε:
 και λόγω της (2), θα είναι
και λόγω της (2), θα είναι  (3)
(3)Από τις (1) και (3) έχουμε:


Άρα:

 .(4)
.(4)Αν είναι
 , τότε θα είναι και
, τότε θα είναι και  και προφανώς τα ορθογώνια τρίγωνα είναι ίσα
και προφανώς τα ορθογώνια τρίγωνα είναι ίσαΑν είναι
 , τότε θα είναι και
, τότε θα είναι και  και η (4) μας δίνει
και η (4) μας δίνει  . Συνεπώς έχουμε το σύστημα:
. Συνεπώς έχουμε το σύστημα:

Με πρόσθεση κατά μέλη παίρνουμε:
 και με αφαίρεση
και με αφαίρεση  , οπότε και πάλι τα τρίγωνα είναι ίσα
, οπότε και πάλι τα τρίγωνα είναι ίσα- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Δύο ορθογώνια τρίγωνα
Καλησπέρα σε όλους. Επιχειρώ μια ακόμα προσέγγιση με διαφορετικά εργαλεία.
Είναι Έστω
Έστω  , οπότε
, οπότε ![\displaystyle \varphi ,\omega \in \left( {0,\;\frac{\pi }{4}} \right] \displaystyle \varphi ,\omega \in \left( {0,\;\frac{\pi }{4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e45c187aa4844dd960cb195d9477b30a.png) .
.
Ισχύει (1)
(1)
και (2)
(2)
Οπότε, από (1) και (2) είναι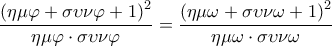 (3)
(3)
Η συνάρτηση![\displaystyle f\left( x \right) = \frac{{{{\left( {\eta \mu x + \sigma \upsilon \nu x + 1} \right)}^2}}}{{\eta \mu x \cdot \sigma \upsilon \nu x}},\;\;x \in \left( {0,\;\frac{\pi }{4}} \right] \displaystyle f\left( x \right) = \frac{{{{\left( {\eta \mu x + \sigma \upsilon \nu x + 1} \right)}^2}}}{{\eta \mu x \cdot \sigma \upsilon \nu x}},\;\;x \in \left( {0,\;\frac{\pi }{4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/28833e28f39b6fd2bfb74eef6c750b94.png)
έχει παράγωγο

με το ίσον μόνον όταν , άρα είναι γνησίως φθίνουσα, οπότε “1-1”, άρα η (3) δίνει
, άρα είναι γνησίως φθίνουσα, οπότε “1-1”, άρα η (3) δίνει  που συνεπάγεται άμεσα ότι τα τρίγωνα είναι ίσα.
που συνεπάγεται άμεσα ότι τα τρίγωνα είναι ίσα.
Είναι
 Έστω
Έστω  , οπότε
, οπότε ![\displaystyle \varphi ,\omega \in \left( {0,\;\frac{\pi }{4}} \right] \displaystyle \varphi ,\omega \in \left( {0,\;\frac{\pi }{4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e45c187aa4844dd960cb195d9477b30a.png) .
.Ισχύει
 (1)
(1)και
 (2)
(2)Οπότε, από (1) και (2) είναι
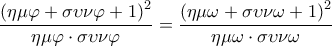 (3)
(3)Η συνάρτηση
![\displaystyle f\left( x \right) = \frac{{{{\left( {\eta \mu x + \sigma \upsilon \nu x + 1} \right)}^2}}}{{\eta \mu x \cdot \sigma \upsilon \nu x}},\;\;x \in \left( {0,\;\frac{\pi }{4}} \right] \displaystyle f\left( x \right) = \frac{{{{\left( {\eta \mu x + \sigma \upsilon \nu x + 1} \right)}^2}}}{{\eta \mu x \cdot \sigma \upsilon \nu x}},\;\;x \in \left( {0,\;\frac{\pi }{4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/28833e28f39b6fd2bfb74eef6c750b94.png)
έχει παράγωγο

με το ίσον μόνον όταν
 , άρα είναι γνησίως φθίνουσα, οπότε “1-1”, άρα η (3) δίνει
, άρα είναι γνησίως φθίνουσα, οπότε “1-1”, άρα η (3) δίνει  που συνεπάγεται άμεσα ότι τα τρίγωνα είναι ίσα.
που συνεπάγεται άμεσα ότι τα τρίγωνα είναι ίσα.- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Δύο ορθογώνια τρίγωνα
Το πρόβλημα ανάγεται στο να κατασκευαστεί ορθογώνιο τρίγωνο με περίμετρο  και εμβαδόν
και εμβαδόν 
Επί της πλευράς ορθής γωνίας
ορθής γωνίας  θεωρώ σημείο
θεωρώ σημείο  τέτοιο ώστε
τέτοιο ώστε  Στο
Στο  υψώνω κάθετο
υψώνω κάθετο
προς την που τέμνει τη διχοτόμο της ορθής στο
που τέμνει τη διχοτόμο της ορθής στο  Γράφω τον κύκλο
Γράφω τον κύκλο  και τον κύκλο
και τον κύκλο  που είναι
που είναι
εγγεγραμμένος στην ορθή και έχει ακτίνα Η κοινή εσωτερική εφαπτομένη των δύο κύκλων τέμνει τις
Η κοινή εσωτερική εφαπτομένη των δύο κύκλων τέμνει τις 
στα Το τρίγωνο
Το τρίγωνο  είναι το ζητούμενο.
είναι το ζητούμενο.
Το τρίγωνο αυτό όπως προκύπτει από την κατασκευή είναι μοναδικό (κατά μέγεθος) και κάθε άλλο ορθογώνιο τρίγωνο με ίδια περίμετρο και ίδιο εμβαδόν, θα είναι ίσο με αυτό.
 και εμβαδόν
και εμβαδόν 
Επί της πλευράς
 ορθής γωνίας
ορθής γωνίας  θεωρώ σημείο
θεωρώ σημείο  τέτοιο ώστε
τέτοιο ώστε  Στο
Στο  υψώνω κάθετο
υψώνω κάθετοπρος την
 που τέμνει τη διχοτόμο της ορθής στο
που τέμνει τη διχοτόμο της ορθής στο  Γράφω τον κύκλο
Γράφω τον κύκλο  και τον κύκλο
και τον κύκλο  που είναι
που είναιεγγεγραμμένος στην ορθή και έχει ακτίνα
 Η κοινή εσωτερική εφαπτομένη των δύο κύκλων τέμνει τις
Η κοινή εσωτερική εφαπτομένη των δύο κύκλων τέμνει τις 
στα
 Το τρίγωνο
Το τρίγωνο  είναι το ζητούμενο.
είναι το ζητούμενο.Το τρίγωνο αυτό όπως προκύπτει από την κατασκευή είναι μοναδικό (κατά μέγεθος) και κάθε άλλο ορθογώνιο τρίγωνο με ίδια περίμετρο και ίδιο εμβαδόν, θα είναι ίσο με αυτό.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες
