Καλησπέρα σε όλους. Αφού άρεσε στον
Θανάση η τριγωνομετρική λύση του
Μιχάλη, παίρνω θάρρος να το τερματίσω:
Χρησιμοποιώ πολικές συντεταγμένες για να έχουμε μονοπαραμετρική συνάρτηση εμβαδού, προσδιορισμό των κορυφών του τριγώνου με τομές ευθειών και αξόνων και για κορύφωση την τραβηγμένη από τα μαλλιά αλγεβρική μέθοδο προσδιορισμού μεγίστου.

- 22-01-2022 Γεωμετρία.png (23.17 KiB) Προβλήθηκε 288 φορές
Έστω

οπότε

.
Είναι

Βρίσκουμε

Είναι

, οπότε

Είναι

και

οπότε

.
Θέλουμε το μέγιστο του

για

.
Επειδή το άθροισμα

είναι σταθερό, το γινόμενό τους θα έχει μέγιστο όταν είναι

(αν γίνεται).
Η ισότητα αυτή ισοδυναμεί με

, οπότε

και για τυχαία ακτίνα

.
 κινείται σε ημικύκλιο , διαμέτρου
κινείται σε ημικύκλιο , διαμέτρου 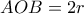 . Το ορθογώνιο τρίγωνο
. Το ορθογώνιο τρίγωνο  , δημιουργείται
, δημιουργείται  τις τομές της
τις τομές της  με την μεσοκάθετη της
με την μεσοκάθετη της  και την προέκταση
και την προέκταση  , ενώ το
, ενώ το  είναι σημείο της ευθείας
είναι σημείο της ευθείας  , με
, με  . Υπολογίστε το
. Υπολογίστε το  .
.
 οπότε
οπότε  . Άρα
. Άρα  ,
,  ,
, 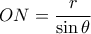 ,
,  .
.
 . Γίνεται με διάφορους τρόπους. Π.χ. έχει παράγωγο
. Γίνεται με διάφορους τρόπους. Π.χ. έχει παράγωγο  , άρα
, άρα  , δηλαδή ισοδύναμα
, δηλαδή ισοδύναμα  .
.  . Τα υπόλοιπα άμεσα. Τελική απάντηση ελαχίστου εμβαδού ίσον
. Τα υπόλοιπα άμεσα. Τελική απάντηση ελαχίστου εμβαδού ίσον  .
.

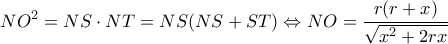

 οπότε η
οπότε η  παρουσιάζει για
παρουσιάζει για 


 . Τα υπόλοιπα άμεσα.
. Τα υπόλοιπα άμεσα. .
. , είναι
, είναι  , που συμπίπτει με την λύση του Γιώργου .
, που συμπίπτει με την λύση του Γιώργου . οπότε
οπότε  .
.

 , οπότε
, οπότε 
 και
και 
 .
. για
για  .
. είναι σταθερό, το γινόμενό τους θα έχει μέγιστο όταν είναι
είναι σταθερό, το γινόμενό τους θα έχει μέγιστο όταν είναι  (αν γίνεται).
(αν γίνεται).  , οπότε
, οπότε  και για τυχαία ακτίνα
και για τυχαία ακτίνα  .
.