 η διχοτόμος,
η διχοτόμος,  το έγκεντρο και
το έγκεντρο και  το περίκεντρο τριγώνου
το περίκεντρο τριγώνου  στο οποίο οι πλευρές
στο οποίο οι πλευρές 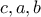 είναι διαδοχικοί όροι αριθμητικής προόδου. Να δείξετε ότι: α)
είναι διαδοχικοί όροι αριθμητικής προόδου. Να δείξετε ότι: α) 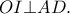
β) Το άθροισμα των αποστάσεων τυχόντος σημείου
 του
του  από τις πλευρές του
από τις πλευρές του  είναι σταθερό.
είναι σταθερό.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 η διχοτόμος,
η διχοτόμος,  το έγκεντρο και
το έγκεντρο και  το περίκεντρο τριγώνου
το περίκεντρο τριγώνου  στο οποίο οι πλευρές
στο οποίο οι πλευρές 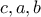 είναι διαδοχικοί όροι αριθμητικής προόδου. Να δείξετε ότι: α)
είναι διαδοχικοί όροι αριθμητικής προόδου. Να δείξετε ότι: α) 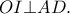
 του
του  από τις πλευρές του
από τις πλευρές του  είναι σταθερό.
είναι σταθερό.i) Ανgeorge visvikis έγραψε: ↑Πέμ Ιουν 29, 2023 11:05 amΠλευρές σε Α.Π..png
Έστωη διχοτόμος,
το έγκεντρο και
το περίκεντρο τριγώνου
στο οποίο οι πλευρές
είναι διαδοχικοί όροι αριθμητικής προόδου. Να δείξετε ότι: α)
β) Το άθροισμα των αποστάσεων τυχόντος σημείουτου
από τις πλευρές του
είναι σταθερό.
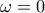 , όπου
, όπου 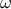 ο λόγος της γεωμετρικής προόδου τότε το πρόβλημα είναι προφανές στο ισόπλευρο τρίγωνο
ο λόγος της γεωμετρικής προόδου τότε το πρόβλημα είναι προφανές στο ισόπλευρο τρίγωνο 
 ii) α) Έστω
ii) α) Έστω 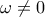 και ας είναι
και ας είναι  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις 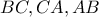 αντίστοιχα,
αντίστοιχα,  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις  αντίστοιχα και
αντίστοιχα και 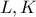 οι ορθές προβολές του περίκεντρου
οι ορθές προβολές του περίκεντρου  του
του  στις
στις  αντίστοιχα (προφανώς τα μέσα των πλευρών αυτών)
αντίστοιχα (προφανώς τα μέσα των πλευρών αυτών) του
του  ισχύει:
ισχύει: 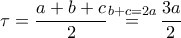 και
και 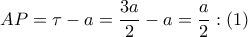 ,
, 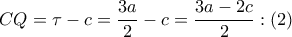
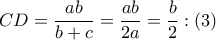
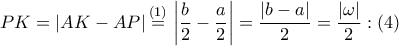 ¨
¨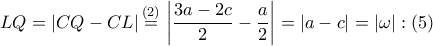 ¨
Από
¨
Από 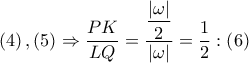 και
και 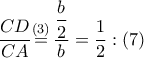 . Από
. Από 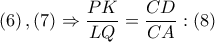 . Τέλος από την
. Τέλος από την  σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι
σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι 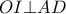 και το πρώτο ζητούμενο έχει αποδειχθεί.
και το πρώτο ζητούμενο έχει αποδειχθεί.  β) Με
β) Με  σημείο της διχοτόμου της γωνίας
σημείο της διχοτόμου της γωνίας  προκύπτει ότι
προκύπτει ότι 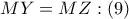
 έχουμε:
έχουμε: 
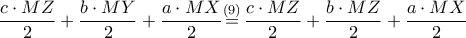
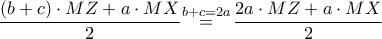
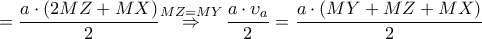
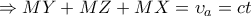 και το δεύτερο ζητούμενο έχει αποδειχθεί.
και το δεύτερο ζητούμενο έχει αποδειχθεί.
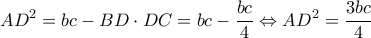

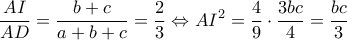

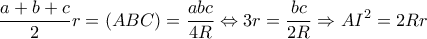
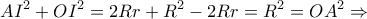
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες