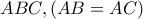 , φέρουμε την διάμεσο
, φέρουμε την διάμεσο  και το ύψος
και το ύψος  ,
,τμήματα τα οποία τέμνουν την διχοτόμο
 στα σημεία
στα σημεία  και
και  αντίστοιχα . Μπορούμε άραγε
αντίστοιχα . Μπορούμε άραγε να κατασκευάσουμε το τρίγωνο αυτό , με τρόπο ώστε να προκύψει :
 ;
;Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
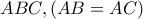 , φέρουμε την διάμεσο
, φέρουμε την διάμεσο  και το ύψος
και το ύψος  ,
, στα σημεία
στα σημεία  και
και  αντίστοιχα . Μπορούμε άραγε
αντίστοιχα . Μπορούμε άραγε  ;
;Το
 είναι το βαρύκεντρο του ισοσκελούς, άρα
είναι το βαρύκεντρο του ισοσκελούς, άρα 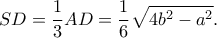 Δίνεται λοιπόν ότι
Δίνεται λοιπόν ότι 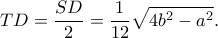 Από 2ο θεώρημα διαμέσου είναι,
Από 2ο θεώρημα διαμέσου είναι, 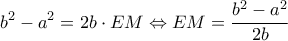 και
και 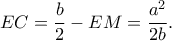
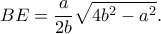 Τέλος, από την ομοιότητα των τριγώνων
Τέλος, από την ομοιότητα των τριγώνων  έχω:
έχω: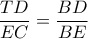 και με αντικατάσταση,
και με αντικατάσταση, 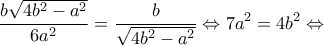
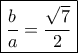
Έστω λυμένο το πρόβλημα . Το
 είναι το βαρύκεντρο του ισοσκελούς
είναι το βαρύκεντρο του ισοσκελούς  .
.  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Λόγω του εγγραψίμου τετραπλεύρου
. Λόγω του εγγραψίμου τετραπλεύρου 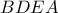 θα έχω :
θα έχω : και αφού
και αφού 
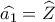 συνεπώς ,
συνεπώς , 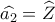 . Ενώ αν θέσω ,
. Ενώ αν θέσω , 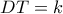 θα είναι :
θα είναι : 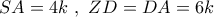 .
.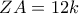 με μέσο το
με μέσο το  . στο
. στο  θεωρώ σημείο
θεωρώ σημείο  με
με 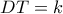 .
.  και την κάθετο στο
και την κάθετο στο  που τον τέμνει στα
που τον τέμνει στα 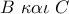 . Το
. Το  είναι αυτό που θέλω .
είναι αυτό που θέλω . .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες