 του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  είναι διάμετρος ημικυκλίου . Οι διχοτόμοι
είναι διάμετρος ημικυκλίου . Οι διχοτόμοι 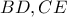
των οξειών γωνιών του τριγώνου , τέμνονται στο
 και η προέκταση της
και η προέκταση της  , τέμνει το τόξο στο σημείο
, τέμνει το τόξο στο σημείο  .
.Επιλέξτε τη θέση του σημείου
 πάνω στο ημικύκλιο , ώστε τα τμήματα :
πάνω στο ημικύκλιο , ώστε τα τμήματα : 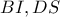 να προκύψουν ίσα .
να προκύψουν ίσα .
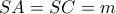 ,
,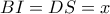 και
και 
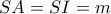 (αφού
(αφού 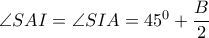 )
)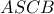 δίνει
δίνει 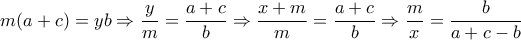
 η
η  θα περάσει από το μέσον
θα περάσει από το μέσον  της
της 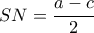
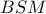 με διατέμνουσα
με διατέμνουσα 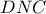 δίνει
δίνει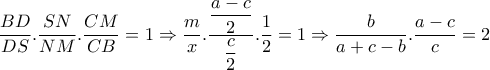
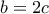
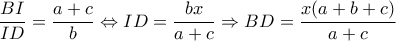
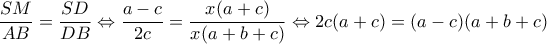
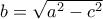 δίνει
δίνει 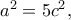 ή αλλιώς
ή αλλιώς 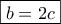 απ' όπου εντοπίζεται το
απ' όπου εντοπίζεται το 