 , της διαμέτρου
, της διαμέτρου  ενός ημικυκλίου , θεωρώ σημείο
ενός ημικυκλίου , θεωρώ σημείο  , τέτοιο ώστε :
, τέτοιο ώστε :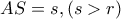 και φέρω την εφαπτομένη
και φέρω την εφαπτομένη  , η οποία τέμνει την προέκταση της
, η οποία τέμνει την προέκταση της  στο σημείο
στο σημείο  .
.α) Υπολογίστε τον λόγο :
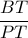 ... β) Για ποια θέση του
... β) Για ποια θέση του  , προκύπτει :
, προκύπτει : 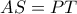 ;
;γ) Υπολογίστε το τμήμα
 ... δ) Προαιρετικό : Για ποια θέση του
... δ) Προαιρετικό : Για ποια θέση του  , θα είναι :
, θα είναι : 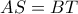 ;
;
 το κέντρο του ημικυκλίου. Από την ομοιότητα των τριγώνων
το κέντρο του ημικυκλίου. Από την ομοιότητα των τριγώνων 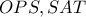 έχω:
έχω: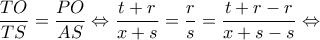
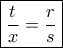
 θα είναι και
θα είναι και 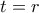 κι επειδή
κι επειδή 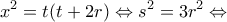
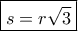
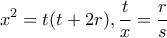 και με απαλοιφή του
και με απαλοιφή του  βρίσκω
βρίσκω 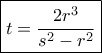

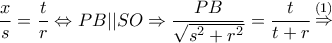
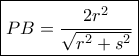
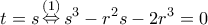 και με λογισμικό,
και με λογισμικό, ![\boxed{s = \left( {\sqrt[3]{{1 - \frac{{\sqrt {78} }}{9}}} + \sqrt[3]{{1 + \frac{{\sqrt {78} }}{9}}}} \right)r \simeq 1,5214r} \boxed{s = \left( {\sqrt[3]{{1 - \frac{{\sqrt {78} }}{9}}} + \sqrt[3]{{1 + \frac{{\sqrt {78} }}{9}}}} \right)r \simeq 1,5214r}](/forum/ext/geomar/texintegr/latexrender/pictures/05c88a7b884b89573da132a05cf14365.png)