Μία ορθή ακόμη

KARKAR · #1

: Μια ορθή ακόμη.png (17.64 KiB) Προβλήθηκε 276 φορές

Στο σκαληνό και οξυγώνιο τρίγωνο ABC

, φέραμε τα ύψη AD , BE , CZ

. Στην

θεωρούμε σημείο

,

τέτοιο ώστε : SC=BD

. Ο κύκλος (D , S , E)

τέμνει το

, στο σημείο

. Δείξτε ότι : $\widehat{TZD}=90^\circ$ .

Μιχάλης Τσουρακάκης · #2

KARKAR έγραψε: ↑
Δευ Μαρ 18, 2024 7:52 pm
Μια ορθή ακόμη.pngΣτο σκαληνό και οξυγώνιο τρίγωνο , φέραμε τα ύψη . Στην θεωρούμε σημείο ,

τέτοιο ώστε : . Ο κύκλος τέμνει το , στο σημείο . Δείξτε ότι : $\widehat{TZD}=90^\circ$ .

Λόγω των εγγράψιμμων HZBD,DHEC,DEMS

η ισότητα των μπλε γωνιών είναι προφανής ,άρα MS//AB

Η

είναι διχοτόμος της γωνίας ZDE

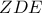του ορθικού τριγώνου ZDE

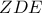και όλες οι γωνίες $\theta$ είναι ίσες.

Ακόμη, $\angle \theta = \angle \phi$ (βαίνουν στο ίδιο τόξο του κύκλου (D,S,E)

) άρα

Αν τώρα

θα είναι $\angle TQZ= \angle \theta$ το ZTDQ

είναι εγγράψιμμο

Ισχύει $\dfrac{AQ}{QB} = \dfrac{AT}{TH}= \dfrac{AM}{MC} \Rightarrow QM//BC$ και το

QBSM

είναι παραλ/μμο ,άρα QB=MS

και προφανώς τα τρίγωνα

QBD,MSC

είναι ίσα άρα $\angle QDB= \angle C= \angle BZD$

Έτσι, η

εφάπτεται του κύκλου (T,Z,Q,D)

κι αφού είναι κάθετη στην

η

θα είναι διάμετρός του, άρα $\angle DZT=90^0$

: Μια ορθή ακόμη.png (56.84 KiB) Προβλήθηκε 173 φορές

Al.Koutsouridis · #3

KARKAR έγραψε: ↑
Δευ Μαρ 18, 2024 7:52 pm
Μια ορθή ακόμη.pngΣτο σκαληνό και οξυγώνιο τρίγωνο , φέραμε τα ύψη . Στην θεωρούμε σημείο ,

τέτοιο ώστε : . Ο κύκλος τέμνει το , στο σημείο . Δείξτε ότι : $\widehat{TZD}=90^\circ$ .

Έστω

το δεύτερο σημείο τομής του κύκλου (D , S , E)

με την πλευρά

και

το ορθόκεντρο του τριγώνου ABC

. Από τα εγγεγραμμένα τετράπλευρα ABDE

και

έχουμε $\angle CSF = \angle FED=\angle ABC$ . Οπότε SF || AB

.

Επίσης έχουμε $\angle EFT = \angle EDT = \angle EDA = \angle EBA = \angle EBZ =\angle ECZ$ . Άρα και FT ||CZ

Οπότε θα ισχύει $\dfrac{HT}{AH} =\dfrac{CF}{AC} \Rightarrow HT = \dfrac{AH \cdot CF}{AC}$ (1)

Στο εγγεγραμμένο τετράπλευρο ACDZ

ισχύει $ZH \cdot HC = AH \cdot HD \Rightarrow ZH = \dfrac{AH \cdot HD}{HC}$ (2)

Διαιρώντας κατά μέλη τις (1) και (2) βρίσκουμε

$\dfrac{ZH}{HT} = \dfrac{AH \cdot HD \cdot AC}{AH \cdot CF \cdot HC} = \dfrac{HD}{HC} \cdot \dfrac{AC}{CF}$ (3)

Από την ομοιότητα των ορθογώνιων τριγώνων HCD

και

, έχουμε $\dfrac{HD}{HC}= \dfrac{BD}{AB}$ και από την παραλληλία των ευθειών FS, AB

έχουμε $\dfrac{AC}{CF} = \dfrac{BC}{CS} = \dfrac{BC}{BD}$ . Οπότε η σχέση (3) γινεται

$\dfrac{ZH}{HT} = \dfrac{BD}{AB} \cdot \dfrac{BC}{BD} = \dfrac{BC}{AB}$

Όμως $\angle ZHT = \angle CHD = \angle B$ . 'Αρα τα τρίγωνα ABC

και

είναι όμοια. Οπότε, $\angle ZTH = \angle A$ .

Άρα έχουμε $\angle ZTH +\angle ZDT = \angle A +\angle ZDA = \angle A+\angle ZCA = 180^0-\angle AZC = 90^0$ .

Επομένως $\angle TZD = 180^0- \left ( \angle ZTH +\angle ZDT \right ) = 180^0-90^0=90^0$ .

: mia_orthh_akomh.png (153.89 KiB) Προβλήθηκε 171 φορές

Μία ορθή ακόμη

Μία ορθή ακόμη

Re: Μία ορθή ακόμη

Re: Μία ορθή ακόμη

Μέλη σε σύνδεση